A Short Review on Fokker-Planck Equations, Entropy Production and Entropy Generation
Jedeshkeran Chandrasegaran, Preet Sharma1
Affiliation
1Non-Linear Science Research Group
2Department of Chemistry & Physics, Midwestern State University
Corresponding Author
Dr. Preet Sharma, Non-Linear Science Research Group. E-mail: jchandrasegar0226@my.msutexas.edu, preet.sharma@msutexas.edu
Citation
Preet Sharma. A Short Review on Fokker-Planck Equations, Entropy 2 Production and Entropy Generation. (2020) J Bioinform Proteom Imaging Anal 4(1): 21-24.
Copy rights
© 2020 Preet Sharma. This is an Open access article distributed under the terms of Creative Commons Attribution 4.0 International License.
Abstract
The Fokker-Planck equation describes the time evolution of the probability density of Brownian particles. These defferential equations are used to model many real life problems in physics, biology, chemistry and engineering. In non-equilibrium thermo-dynamics, the energy generation and energy production approach has been very important tools in describing systems. We have written a brief review on both these methhods andexplained the connection with Fokker-Planck equations with the entropy generation and entropy production method.
Introduction
There has been a considerable rise in the number of studies in which the principles of non-equilibrium statistical physics and related fields can be applied to understand other fields such as biology, chemistry and engineering. This interdisciplinary field has been very active in the last decade or so and the scientific community has contributed considerably towards this goal. In this context, the Fokker-Planck equation is a good tool, and it represents the probability density for the position or velocity of a particle of which the motion is described by a corresponding Langevin equation (Lucia 2014). Since the entropy of a system always increases, the Fokker-Planck equation can be used to calculate the entropy. The Fokker-Planck equations have a wide range of applications leading to many interdisciplinary studies. This review paper discusses the entropy generation, entropy production approach and the Fokker-Planck equation.
Non-Equilibrium Fokker-Planck Equation
Consider a set of n interacting particles. Let the particles evolve with time through the Langevin equations given by
![]()
where xi is the position of the ith particle, x = {xi}, fi(x) is the force acting on the ith particle, ri is the noise that is mathematically considered to be a stochastic variable such that
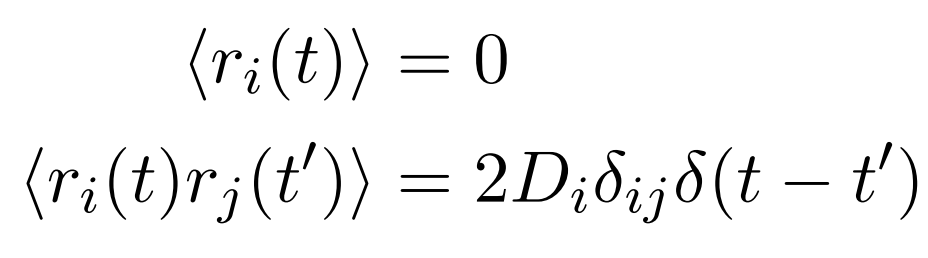
with Di ≥ 0, different constants for each particle.The associated Fokker-Planck equations describe how the probability distribution, P (x, t) evolves with time (Tome 2006). This can be written as
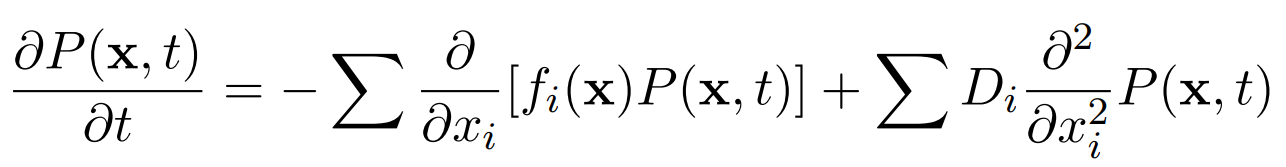
We can write down the Fokker-Planck equation in a more convenient way as a continuity equation,
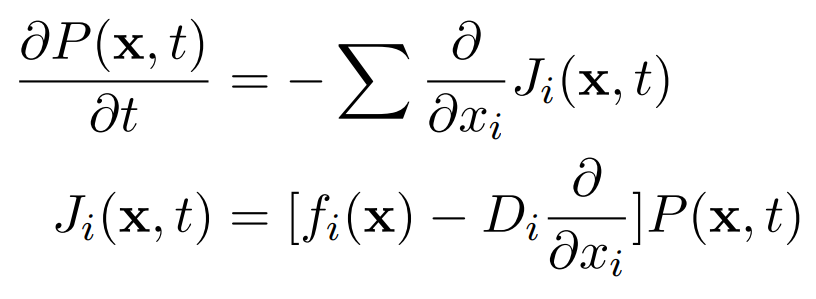
where Ji is the ith component of the current of probability The condition of irreversibility can be expressed as
![]()
or
![]()
but
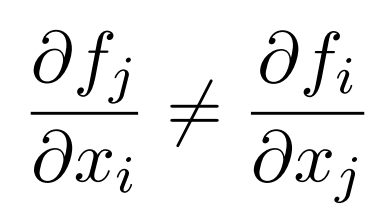
The Fokker-Planck equation has to be solved inside a given region of the space spanned by the set of variables xi subject to a prescribed boundary condition which governs the behavior of P(x, t) and Ji(x, t). In the thermodynamic equilibrium case the Langevin equationand the associated Fokker-Planck equations, which describe a system where
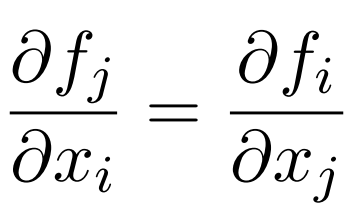
for any pair i and j
Di = Dj
Derivation of Fokker-Planck Equation
Starting from eqn. (2.1) which is the Langevin equation,
![]()
Consider a particle at a position x at time t. After a small time δt the particle would have moved a small amount given by
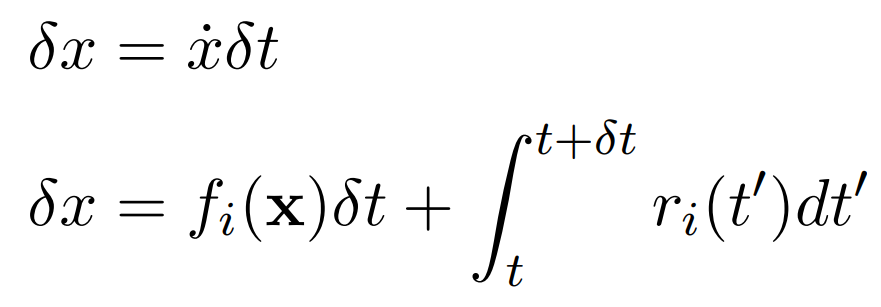
here we have taken the average of the noise function and also assummed that δx is very small. Sice the average of the noise function is zero eqn.(3.3) becomes
![]()
and so we can write
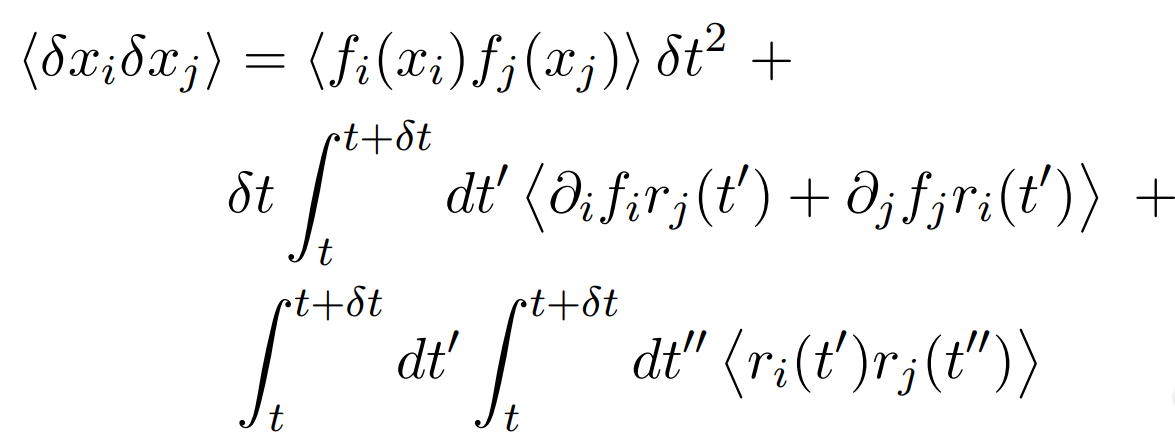
using eqn.(2.3) the last term on the right hand side of eqn.(3.5) gives
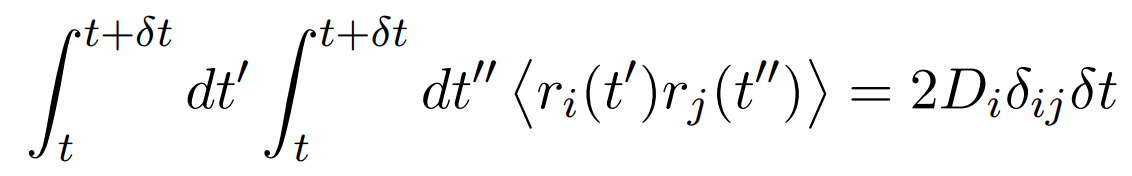
the first two terms on the right hand side of eqn.(3.5) are of order (δt)2 and hence can be neglected. So we can write eqn.(3.5) as
![]()
Now we have to find a probability distribution function which can give us eqn.(3.4) and eqn.(3.7). For that purpose, let us consider the conditional probability P(x, t + δt; x', t). This probability is defined as the probability that the particle is at position x at time t+δt given that at a small time δt earlier it was at position x'. From definition we know that
![]()
where δx is a small change in position corresponding to δt. The Taylor series for a function f(x) is written as
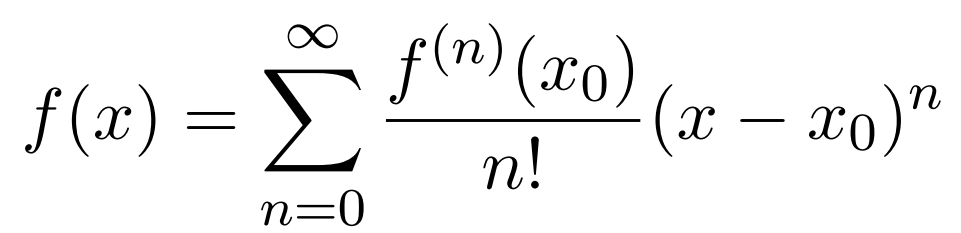
for the right hand side of eqn.(3.8) we can write
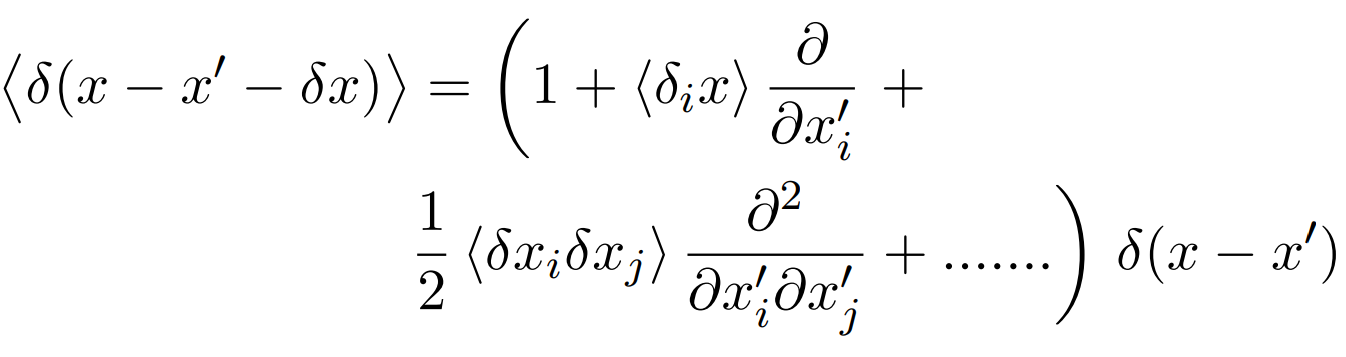
now we will make use of the Chapman-Kolmogorov equation according to which
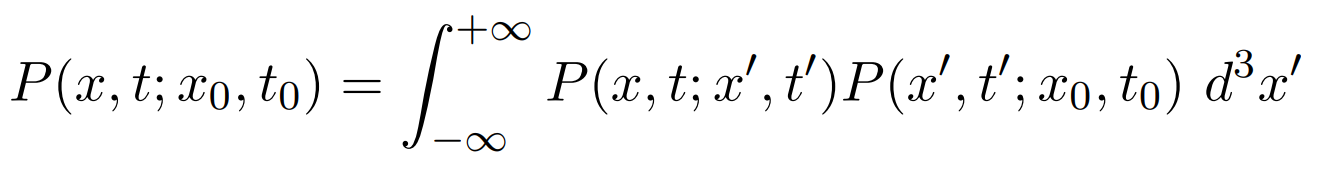
where x0 is the value of x at t0 and x', t' are values at any intermediate step. Using this we can write
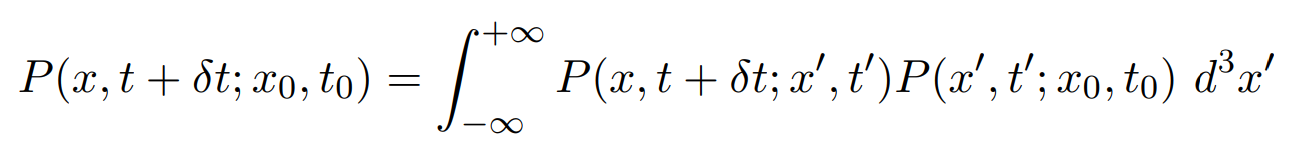
using eqns. (3.8) and (3.10) we can write
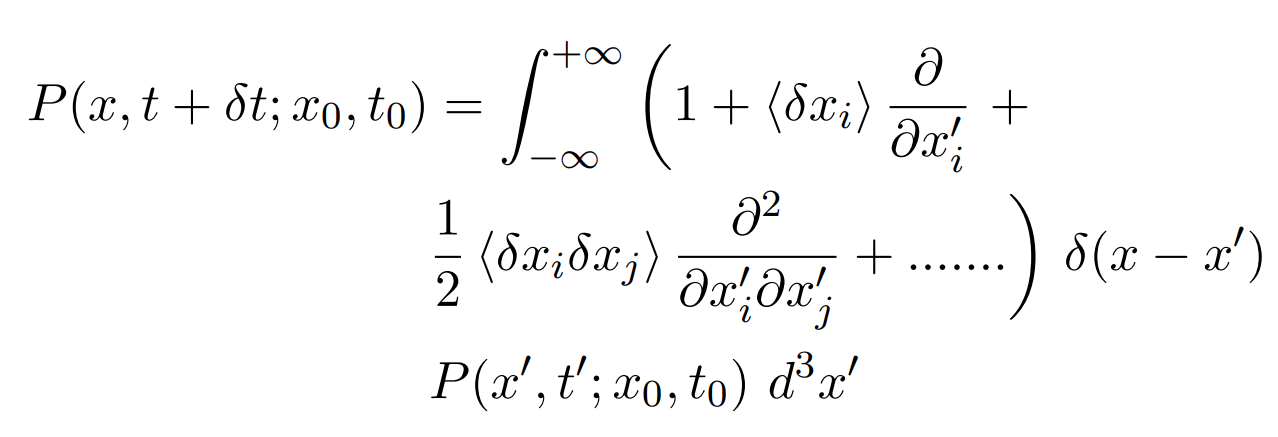
simplifying and rearranging the terms we get,
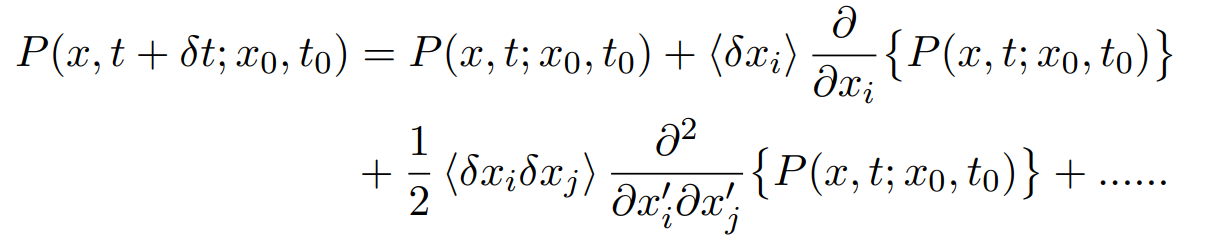
using eqn.(3.4) we can write
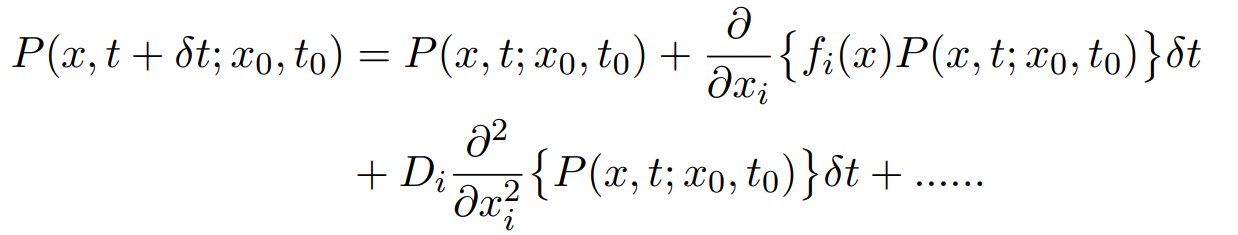
simplifying this further we get
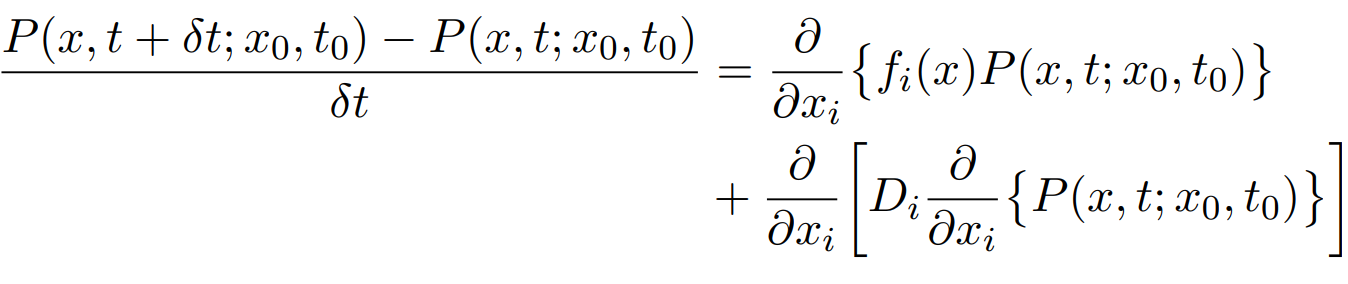
and hence
![]()
where
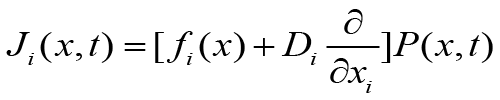
This is the Fokker-Planck equation and they describe the time evolution of the probability distribution P(x, t).
Entropy Production and Fokker-Planck Equations
The rate of change of the entropy S of a system can be written as (Nicolas & Prigogine 1997)
dS/dt= ς-Ω
where ς is the entropy production due to the irreversible processes in the system and Ω is the entropy flux from the system to the environment. In an equilibrium system entropy is a well defined quantity but in non-equilibrium systems the entropy as well as the production of entropy is not well defined. Since a non-equilibrium system is defined by the Fokker-Planck equations, we have attempted to calculate the production of entropy in such systems. Here we use the Gibbs entropy because the Gibbs entropy does not require the system to be single or well defined state. The Gibbs entropy of a system at any time t is given by (Tome 2006)
![]()
where dx = dx1dx2......dxn. Using eqn. (2.5) we can express the derivative of the entropy as
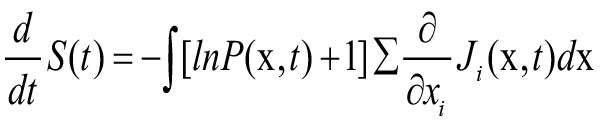
Integrating we get
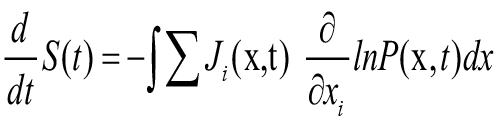
using eqn. (2.6) we can write
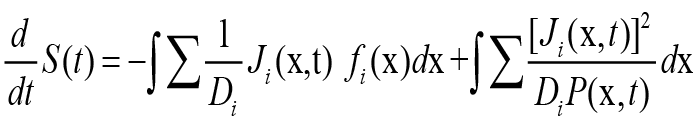
comparing this with eqn. (3.1) we see that
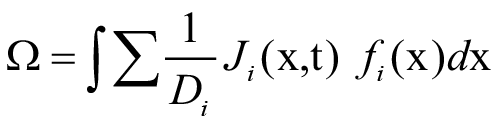
and
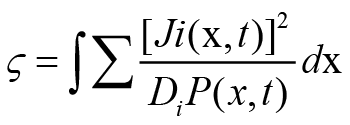
Using eqn. (2.6) we can write eqn. (3.6) as
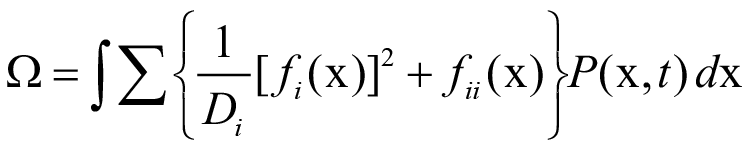
where fii(x) = ∂fi(x)/∂xi. This can be expressed as an average over the probability distribution.
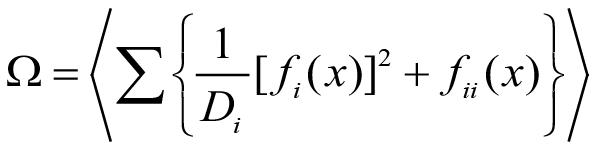
Entropy Generation and Fokker-Planck Equations
It has been discussed by Jaynes that Gibbs’ formalism for statistical physics of systems under equilibrium can be understood as a generalized form in a statistical inference theory for non-equilibrium systems (Dewar 2003). Jaynes developed non-equilibrium statical physics for the stationary state constraint on the basis of maximum entropy, and his approach consisted of maximizing the path. The Shannon information entropy for the path can be written as
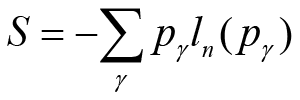
with respect to pγ of the path γ. According to Shannon, the information entropy can be written as the logarithm of the number of outcomes i with non negligible probability pi, while in non-equilibrium statistical physics it is the given as the logarithm of the number of microscopic phase-space paths γ having non negligible probability pγ (Dewar 2003; Lucia 2014) Following this approach, we know that the information entropy for open systems is related to their entropy generation by (Lucia 2008; 2009; 2010)
![]()
with Pγ = Pγ(x, t). This relation is the statistical definition of entropy generation. This can also be explained as the missing information which is necessary for predicting which path a system of the ensemble takes during the transition from one state to another. The Guoy-Stodola theorem (Lucia 2014) gives
W¯=T0Sg
where W¯ is work lost due to internal irreversibility in a system. By definition, the entropy generation can be related to the power lost, P due to irreversibility,
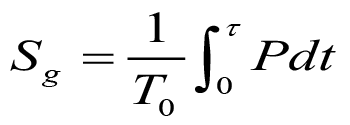
where T0 is the environmental temperature, considered constant and τ is the time duration of a physical process. The power lost by definition is given as,
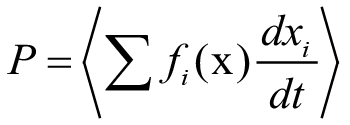
Using the Langevin equation we can write this as
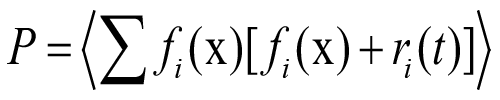
and so Sg can be written as
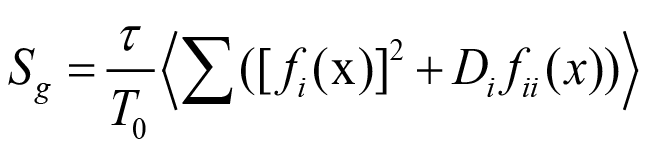
where fii =∂fi/∂xi Considering the mean value, we can finally write this as
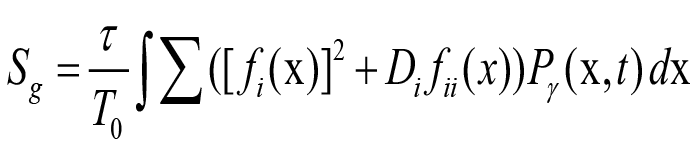
and hence
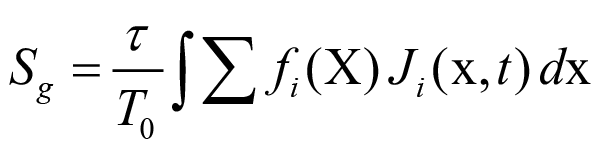
where the last term is related with the Fokker-Planck equation.
Conclusion
In this review paper we have studied the Fokker-Planck equation and derived them. The principles of statistical physics allow a connection between the Fokker-Planck equations and the different entropy approaches. Our future work will be to apply the Fokker-Planck equations and the enytropy approaches to systems which exhibit a non-equilibrium physics behavior. By doing so we will be able to understand such systems better.
References
- 1. Nicolas, G., Prigogine, I. Self-Organization in Nonequilibrium Systems. (1997) Bifurcation Analysis 3-12.
PubMed│CrossRef│Others
- 2. Richard, J., David, K., Felix, O. The variational formulation of the Fokker-Planck equation. (1996) SIAM J MATH ANAL 29(1):1-17.
PubMed│CrossRef│Others
- 3. Cohen, M.B., Grieblin, T.L., Ahaghotu, C.A., et al. Cellular adhesion molecules in urologic malignancies. (1997) Amer J Clin Pathol 107(1): 56-63.
- 4. Solomon, K.A. Physics and Cancer. (2002) Physics Today 55(9): 52.
- 5. Dewar, R. Information theory explanation of the uctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. (2003) J Phys A: Math Gen 36: 631-641.
- 6. Okegawa, T., Pong, R., Li, Y., et al. The role of cell adhesion molecule in cancer progression and its application in cancer therapy. (2004) Acta Biochim Pol 51(2): 445-457.
- 7. Tome, A. Entropy production in nonequilibrium systems described by a Fokker-Planck equation. (2006) Braz J Phys 36(4): 1285-1289.
- 8. Lucia, U. Statistical approach of the irreversible entropy variation. (2008) Physica A: Statistical Mechanics and its Applications. 387(14): 3454-3460.
- 9. Lucia, U. Irreversibility, entropy and incomplete information. (2009) Physica A: Statistical Mechanics and its Applications. 388(19): 4025-4033.
- 10. Lucia, U. Maximum entropy generation and exponential model. (2010) Physica A Statistical Mechanics and its Applications 389(21): 4558-4563.
- 11. Lucia, U. Entropy Generation and the Fokker-Planck Equation. (2014) Physics A Statistical Mechanics and its Applications 393(1): 256-260.
- 12. Levine, H. Introduction to Physics in Cancer Research. (2014) Cancer Research 74(17): 4572-4573.
- 13. Klopper, A. Topics in Non-Equilibrium Physics. (2015) Nature Physics Insight 11(2): 103.
PubMed│CrossRef│Others












