Biological radiation effects involve all levels in the hierarchy of biological organization^[1]. Radiation induces the energy absorption in atoms and molecules essential to life, and the resulting deletions of DNA are the major contributors to the mutations driving radiation carcinogenesis^[2]. Usually, biological radiation effects are estimated from epidemiological data^[3], owing mainly to life span studies on atomic bomb survivors^[4]. In spite of this fact, for low dose radiation effects, the statistical capability of epidemiological analysis has limitations^[2,3]. Hence, cellular and molecular biology data have also been needed to estimate radiation effects^[2]. The main endpoints in epidemiological studies are the cancer incidence rate and the mortality rate^[5], while those in cellular and molecular biology are indices about DNA damage and cell survival^[6,7]. In both areas, macroscopic and microscopic, how these endpoints are affected by radiation dose has been investigated. Epidemiologists have also investigated the relationship between the macroscopic endpoints and the effect modifiers such as attained age, age at exposure, smoking and so on^[4,8,9], while cellular and molecular biologists have investigated the relationship between the microscopic endpoints and some genes or proteins^[6]. Up to now, while many studies have been conducted to elucidate the biological effects of radiation as above, there still exists a significant gap between epidemiology and cellular or molecular biology. In epidemiology, some researchers have proposed microscopic mathematical models to explain macroscopic phenomena^[10]. However, the correspondence of model parameters to the microscopic experimental variables in cellular or molecular observation is unclear. In cellular and molecular biology, some studies have found those salient phenomena such as bystander effects and hypersensitive cellular responses^[11,12], and the microscopic mechanisms of these phenomena have been investigated. The application of such studies is mainly to the radiotherapy for cancer and the exposure estimation^[13-15]. However, researchers in this field rarely use the data on cancer risk. Therefore, the relationship of the adverse effects at human scale with microscopic phenomena such as cell death and DNA lesions is not elucidated.

  Finding a microscopic index which corresponds directly to the impact of radiation on health risk would then provide a better measure for the estimation of radiation effects. We have thus investigated the microscopic index which may be correlated with the cancer incidence rate. The viewpoint in this study is as follows. Dead cells, even if they have a number of DNA lesions, will not induce delayed effects, while survival cells that have DNA lesions would do. Here, we introduce two indices associated with cell survival and DNA lesions. One is the number of cells which survive and suffer from one or more double strand breaks (DSBs) of DNA. The other is the total number of DNA DSBs among all survival cells.

  In this paper, we estimate the dependence of the two indices on the radiation dose in terms of a statistical model constructed from the existing data for each of the number of DSBs and the fraction of cell survival. Then, we compare these two dose dependences with that of solid cancer incidence rate calculated with atomic bomb survivor data. Moreover, we calculate the correlation coefficients between the cancer incidence rate and four microscopic indices which include the two new indices described above and conventional ones of cell survival and DSBs to determine which indicator would correspond directly to radiation risk most appropriately. In the following sections, the underlying probability theory and the calculated results will be shown along with pertinent discussions.

Materials and Methods

  We consider a system of N_ir cells exposed to acute radiation with dose d. Then some DNAs may be damaged in the cells. The mean number of DSBs per cell, L, is assumed to be proportional to dose^[16],
L(d) = a ∙ d     (1)

where a is the mean number of DSBs per cell per radiation dose. Probability that a cell suffers l DSBs will be described by the Poisson distribution^[17],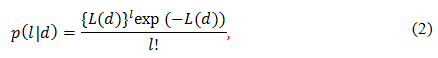

  assuming that the effect of different particles of the radiation is independent of each other. Moreover, some cells will lose their proliferative potential, where such cells will be called “dead” cells. The “survival” cell fraction s is defined as the fraction of cells retaining this potential. The survival fraction curve refers to the relationship between the survival fraction and the radiation dose. We will then adopt the linear-quadratic model^[18],
 s(d) = exp(-α ∙ d - β ∙ d²),    (3)
which is commonly used.

  Dead cells, even if they have a number of DNA lesions, will not induce delayed effects, while survival cells that have DNA lesions may induce the effects. Thus, we consider the probability that a cell survives and also suffers k DSBs when the cell was exposed to the radiation dose d, P(S,B_k |E_d). The conditional probability P(S,B_k |E_d) describes the probability that both S and B_k are true given E_d is true. S is the proposition that a cell survives, B_k is the proposition that a cell suffers k DSBs, and E_d is the proposition that a cell was exposed to the radiation dose d. The quantities p(k|d) and s(d) defined above correspond to the marginal probabilities P(B_k |E_d) and P(S|E_d), respectively:

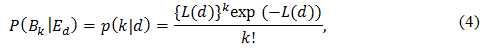
 P(S|E_d) = s(d) = exp(-α ∙ d - β ∙ d²)    (5)

  The previous studies have considered only the marginal probabilities, and we assume that P(S,B_k│E_d) is the product of P(B_k│E_d) and P(S|E_d),
P(S,B_k│E_d) = P(B_k│E_d) ∙ P(S│E_d),   (6)
in the present study. This assumption implies that the cell survival and the number of DSBs are independent of each other as functions of radiation dose.

  We introduce the index Nc_s,b, defined as the number of survival cells which have suffered one or more DSBs. It is the product of the number of cells irradiated, N_ir, and the probability that a cell survives and suffers one or more DSBs at the same time. The latter probability corresponds to P(S,B_̅0│E_d), where B̅ ₀ is the denial of the proposition B₀. According to a probability theory rule, we find
P(S,B̅ ₀│E_d) = P(S│E_d) - P(S,B₀│E_d).    (7)

Therefore, Nc_s,b is given by
Nc_s,b = N_ir ∙ {P(S│E_d) - P(S,B₀│E_d)}.    (8)

  The total number of DSBs among all survival cells, Nb_s, is the second index we introduce in the present study. It is the product of the number of survival cells and the mean number of DSBs that the survival cells suffer. The number of survival cells is the product of the number of irradiated cells, N_ir, and the survival fraction, P(S│E_d) : N_ir ∙ P(S│E_d). On the other hand, the mean number of DSBs that survival cells suffer is the conditional expectation of k given S and E_d, Σ_kk ∙ P(B_k│S,E_d). Therefore, the total number of DSBs among all survival cells, Nb_s, is given by
Nb_s = N_ir ∙ P(S│E_d) ∙ Σ_k k ∙ P(B_k│S,E_d)    (9)
  = N_ir ∙ Σ_k k ∙ P(S,B_k│E_d),    (10)
where we have used the ansatz P(S,B_k│E_d) = P(S│E_d) ∙ P(B_k│S,E_d).

  Hereafter, we will consider indices x ≡ Nc_s,b / N_ir and y ≡ Nb_s / N_ir , where N_ir is an unknown constant. We use Eqs. (4) and (5) for P(B_k│E_d) and P(S│E_d) respectively. Moreover, we employ Eq. (7). Thus, the dose dependences of x and y are represented by

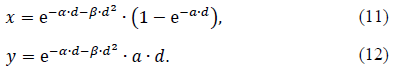
  As for the three parameters, α,β and a appearing in Eqs. (11) and (12), Malaise et al.^[19] estimated α = 0.57 Gy^-1 and β = 0.032 Gy^-2 using the data on many fibroblasts from a variety of organs such as lung, HF19, skin, 1BR and so on, while Rothkamm and Löbrich^[17] estimated α = 37 Gy^-1 by observing γ-H2AX using human fibroblasts from the lung, MRC-5. We will employ these values in the following.

  We used the data on the dose dependence of relative risk about cancer incidence to verify whether the indices we introduced can represent the delayed effect of radiation. Data that we use are taken from life span study for atomic bomb survivors^[4,20] including 25570 subcohorts. Then we stratify the subcohorts on DS02 weighted colon dose and calculate the incidence rate on each subcohort. The incidence rates are calculated by (Σ_i n_i)/ (Σ_iτ_i), where, n_i is the number of incident cancer cases on subcohort i and τ_i is person-time on subcohort i; the standard errors of the incidence rates are then calculated by √(Σ_in_i) / (Σ_iτ_i)).

  Pearson’s product-moment correlation coefficient, r, was used as a measure of the correlation between cancer incidence rate and four microscopic indices. The associated p-value was calculated by Pearson’s correlation test^[21].

Results

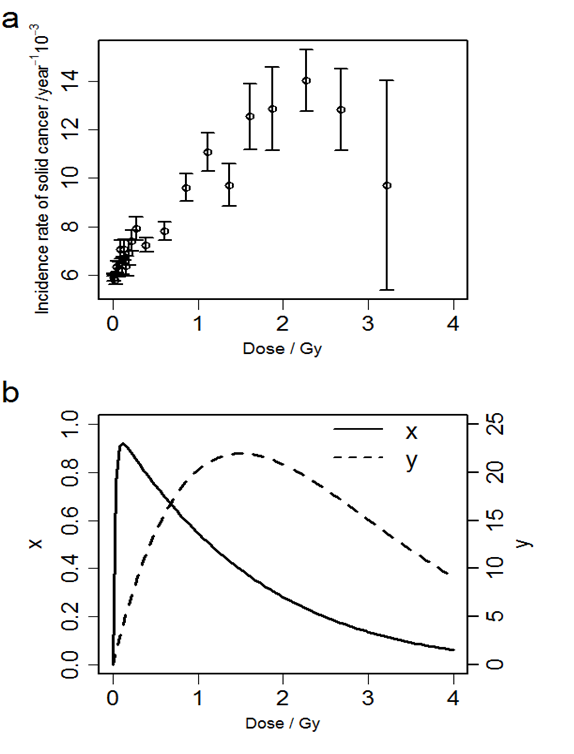
  Figure 1 (a) shows the relationships between the radiation dose and the solid cancer incidence rate. Figure 1 (b) shows the relationship between the radiation dose and two indices we introduced in Equations. (11) and (12). The solid cancer incidence rate is approximately proportional to dose up to about 2 Gy, and the rate tends to decrease at higher dose. The number of cells which survive and suffer one or more DSBs per the number of irradiated cells, x, takes the maximum at about 0.11 Gy, and the total number of DSBs among all survival cells per the number of irradiated cells, y, takes the maximum at about 1.5 Gy.

Figure 1: (a) The relationship between radiation dose and solid cancer incidence rates. Error bar indicates standard error of the incidence rate. (b) The relationships between the dose and x, the number of cells which survive and suffer one or more DSBs per the number of irradiated cells (solid line, left axis), and y, the total number of DSBs among all survival cells per the number of irradiated cells (dashed line, right axis).

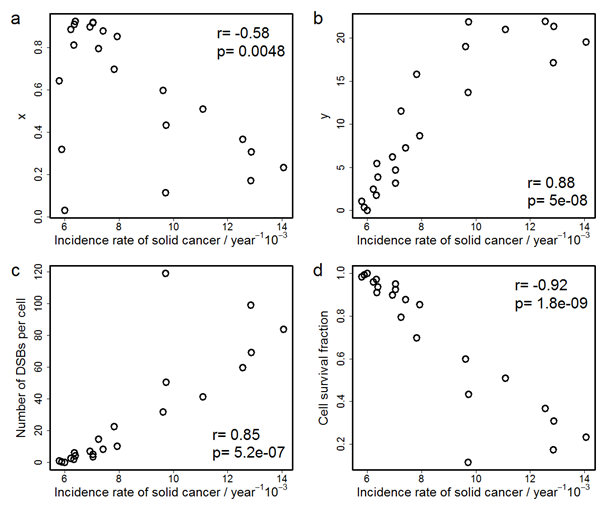
  Figure 2 shows the correlations between the solid cancer incidence rate and x, y, the number of DSBs per cell, and cell survival fraction. The correlation efficient, r, for y, is the largest (+0.88) among the coefficients for the four indices. Discussions concerning these two figures will be given in the following section.

Figure 2: Correlations between the incidence rate of solid cancer and (a) x, the number of cells which survive and suffer one or more DSBs per the number of irradiated cells, (b) y, the total number of DSBs among all survival cells per the number of irradiated cells, (c) the number of DSBs per cell, and (d) cell survival fraction. r is Pearson’s product-moment correlation coefficient and p is p-value on Pearson’s correlation test.

Discussion

  The reason why the dose dependences of x and y have a peak is attributed to the fact that less cells survive at higher dose due to cell deaths. The peak of x appears at the dose where almost all cells have DSBs, and x at the higher dose decreases because of cell death. On the other hand, since the number of DSBs does not saturate unlike the number of DNA-lesioned cells, the peak of y appears at higher dose than that of x. For comparison, the maximum of the solid cancer incidence rate is observed at around 2 Gy, which agrees with a previous study^[4] where the linear model overestimates the incidence rate at high dose. Therefore, the comparison of the doses that give the maximum in their dose-response curves shows that the dose dependence of y is more similar to that of the incidence rate than that of x. This suggests that y is a better indicator of radiation effects on solid cancer incidence than x. Moreover, in order to discuss more quantitatively the correspondences of these indices to the cancer incidence rate and to compare the two indices with conventional indices, such as the number of DSBs per cell or the fraction of survival cells, we calculated the correlation coefficient of the four indices with the solid cancer incidence rate. As a result, the correlation coefficient between the index y and the solid cancer incidence rate is larger than those between other microscopic indices and the solid cancer incidence rate. Although the absolute value of the correlation coefficient for the fraction of survival cells is larger than that of y, the fraction of survival cells is not regarded as a direct measure for cancer. The coefficient for y is larger than the correlation coefficient for the number of DSBs per cell which is proportional to dose. This means that the dose dependence of the incidence rate has the peak rather than being linear. On the other hand, even though the dose dependence of x has the peak, the correlation coefficient for x is smaller than that for the number of DSBs per cell whose dose dependence has no peak. This implies that it is not sufficient that the dose dependence has a peak and the peak position affects the correlation coefficient. Thus, we consider that the peak dose of y corresponds to that of the incidence rate. This suggests that the total number of DSBs among all survival cells is the best indicator of radiation effects among the four indices we consider. It also means that we should consider both cell death and DNA lesions simultaneously to estimate macroscopic radiation risk. In addition, our study indicates that the decrease in the incidence rate at high dose is due to the cell death. Needless to say, the decrease in the incidence rate at high dose does not imply the safety at that dose because the acute lethal effect occurs beyond around 2 Gy^[22].

  Our study suggests that we should consider both cell death and DNA lesions simultaneously to estimate radiation risk. Many researchers have investigated bystander effect and cell hypersensitivity at low dose^[12,23-25]. Some of them have observed either cell death or DNA lesions and aimed to understand the mechanism of the observed phenomena. Moreover, some researchers, even if they observed both cell death and DNA lesions, have not discussed how cell death and DNA lesion interact with each other and affect human health. In contrast, we have introduced a new concept of the total number of DSBs among all survival cells, which is an index associated with both cell death and DNA lesions, giving a new index that is correlated with cancer incidence better than the conventional indices such as cell survival and DNA lesions. In addition, some researchers have proposed models to analyze data on radiation effects, but the parameters in these models have not been compared with the parameters obtained by microscopic observations^[10]. On the other hand, we here use microscopic parameters on cell and molecular biology to estimate the new indices and to analyze cancer incidence data. On the basis of the calculated results in Figure. 2(b), we can derive a regression formula for predicting the incidence rate of solid cancer per 103 person per year, λ, from the total number of DSBs among all survival cells per the number of irradiated cells, y, as
λ = 0.2901y + 5.4871.    (13)

  This study then provides a tool for epidemiologists and cell or molecular biologists to refer to mutual studies. Thus, our index has potential applications for appropriately estimating the impact of radiation on human health.

  Finally, we would like to make a comment on the validity of the present analysis in which biochemical parameter values (a, α and β) obtained from in vitro studies of fibroblasts have been employed. In order to assess the robustness of the present results, we have attempted to use a = 8 Gy^-1 estimated in an in vivo model^[26] instead of a = 37 Gy^-1 employed above. We have then found that the calculated results for Figure. 2 are very similar to those shown above, thus suggesting a robust validity of the present analysis, which should be examined through further studies in the future.

Conclusion

  In summary, we have proposed two novel indices associated with cell death and the number of DSBs in the present study. Compared also with the earlier indices, the total number of DSBs among all survival cells correlates with the cancer incidence rate more relevantly. This suggests that the decrease in the incidence rate at high dose is due to the cell death and that we should consider both cell death and DNA lesions to estimate radiation risk appropriately. Furthermore, the index is estimated using the parameters in microscopic experiment on cell death and DSBs, which enables epidemiologists and cell or molecular biologists to refer to mutual studies. Our study thus provides additional information on radiation effects and a useful tool to discuss radiation effects quantitatively.

Acknowledge:
  This report makes use of data obtained from the Radiation Effects Research Foundation (RERF) in Hiroshima and Nagasaki, Japan. RERF is a private, non-profit foundation funded by the Japanese Ministry of Health, Labor and Welfare (MHLW) and the U.S. Department of Energy (DOE), the latter through the National Academy of Sciences. The data include information obtained from the Hiroshima City, Hiroshima Prefecture, Nagasaki City, and Nagasaki Prefecture Tumor Registries and the Hiroshima and Nagasaki Tissue Registries. The conclusions in this report are those of the authors and do not necessarily reflect the scientific judgment of RERF or its funding agencies.

References