Evaluation of Arterial-Venous Blood Alcohol Concentration Gradients of Ethanol Administered by an Infusion to Dogs
Affiliation
Slovak Academy of Sciences, Institute of Experimental Pharmacology and Toxicology, Bratislava, Slovak Republic
Corresponding Author
Maria Durisova, Slovak Academy of Sciences, Institute of Experimental Pharmacology and Toxicology, Bratislava, Slovak Republic, Tel: 002412; E-mail: maria.durisova@savba.sk
Citation
Maria, D. Evaluation of Arterial Venous Blood Alcohol Concentration Gradients of Ethanol Administered by an Infusion to Dogs. 2018 J Pharma Pharmaceutics 5(1): 40- 43.
Copy rights
© 2018 Maria, D. This is an Open access article distributed under the terms of Creative Commons Attribution 4.0 International License.
Keywords
Dynamic system; Mathematical model
Abstract
Numerous workers investigated ethanol pharmacokinetic. Therefore, the goal of the present study was not an investigation of ethanol pharmacokinetics; instead, the goal of the present study was to prepare further illustrative examples of a successful use of computational and modeling tools from system engineering in pharmacokinetic investigations. The previous study by Wilkinson and Rheingold published in October 1977 issue of the Journal of Pharmacokinetics, described an investigation of arterial-venous blood concentration gradients of ethanol administration by a constant rate intravenous infusion through indwelling venous catheters to dogs. The present study is a free continuation of the study by Wilkinson and Rheingold; therefore, the data available in the study by Wilkinson and Rheingold were used. An advanced modeling method, implemented in the computer program named CTDB, and described in the study by Dedik et al[1] was used for modeling purposes.
Introduction
Ethanol, has been used medicinally and recreationally and its pharmacokinetic properties have bare been studied widely for medical, legal and forensic purposes.
Numerous studies published previously described investigations of the pharmacokinetic behavior of ethanol using traditional pharmacokinetic modeling method[2-8]. Therefore, the goal of the present study was not to investigate ethanol pharmacokinetics; instead, the goal of the present study was to prepare further illustrative examples of a successful use of modeling and computational tools from system engineering in pharmacokinetic investigations. The previous examples can be fin in the full-text articles that are available free of charge at the following web site of the author: http://www.uef.sav.sk/durisova.htm
In the preparation of illustrative examples, the data available in the study by Wilkinson Rheingold and an advanced modeling method implemented In the software named CTDB were used[1].
An example of a successful use of the computer CTDB can be find in the study by Dedík et al. published in September 2007 Issue of the Journal Diabetes Research and Clinical Practice, which is available here:
http://www.uef.sav.sk/advanced_files/OGTT-2007.pdf
The mathematical models developed in the present study, successfully described observed ethanol concentration-time profiles of ethanol of the dogs investigated in the study by Wilkinson and Rheingold[8] and in the present study.
Method
The data of dogs taken from the study by Wilkinson and Rheingold were used.
The advanced mathematical modeling method described in the study by Dedík et al[1], published in September 2007 Issue of the Journal Diabetes Research and Clinical Practice and implemented in the computer program named CTDB was employed for modeling purposes[1]. The demo version of the computer program CTDB can be finding on the following author’s web site: http://www.uef.sav.sk/advanced.htm
The development of mathematical models of the centration-time profiles of ethanol after ethanol infusion to the dogs investigated in the study[2] and in the present study was performed as described later on:
On the first step of the model development process, an ADME related dynamic system was defined in Laplace domain for the dogs, using the transfer function, denoted by H(s) and described by Eq. (1):
(1)
In Eq.(1): S is the Laplace variable, I(s) is the Laplace domain counterpart of the mathematically transformed intravenous administration of ethanol to the dogs[2] and C(s) is the Laplace domain counterpart of the mathematically transformed blood ethanol concentration time profile measured following intravenous administration of ethanol to the dogs investigated in the study[2] and in the present study.
On the second step of the model development process, a mathematical model of the dynamic system defined was developed, using the advanced modeling method implemented in the computer program named CTDB[1].
The general form of the model transfer function HM(s) used also in the present study, is described by the following equation:
(2)
On the right-hand-side of Eq. (2) is the Padé approximant to the model transfer function HM(S) [9,10],
G is an estimator of the model parameter conventionally called a gain of a dynamic system, a1,...an,b1...bm are additional model parameters, n is the highest degree of the numerator polynomial, and m is the highest degree of the denominator polynomial, where n < m see for example the studies[11-27] and references therein.
On the third step of the model development process, the model transfer function was converted into the equivalent model frequency response function (denoted by FM(Iωj)) in the frequency domain; see for example, the studies cited above.
After that, the previously published non-iterative method[28] was employed to determine the model frequency response function FM(Iωj) of the dogs, and to determine point estimates of the parameters of the model frequency response function FM(Iωj) in the frequency domain. The general form of a model the frequency function FM(Iωj) is described by Eq. (3). It was also used in the current study.
(3)
Besides the radial frequency ω and the imaginary unit i, the meaning of the symbols used in Eq. (3) is the same as the meaning of the symbols used in Eq. (2)
On the forth step of the model development process, the best model of the frequency response function FM(Iωj) was selected using the Akaike information criterion, modified for the use in the complex domain[29,30].
On the fifth step of the model development process, a) the output C(s) of the model developed corresponding to the ethanol input I(s) was determined, using a numerical simulation method in the time domain;
After that the model output C(s) was refined, using the Gauss-Newton and Monte-Carlo method[31,32] in the time domain.
After that, the outcomes of the models developed and the concentration-time profiles of ethanol were mutually statistically compared, and in this way, a validation on the models was performed[33-38].
Results
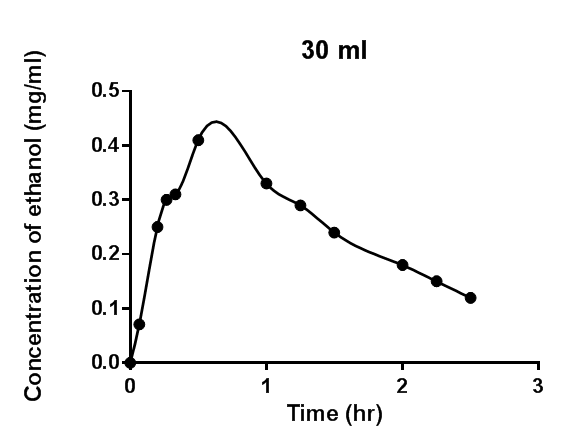
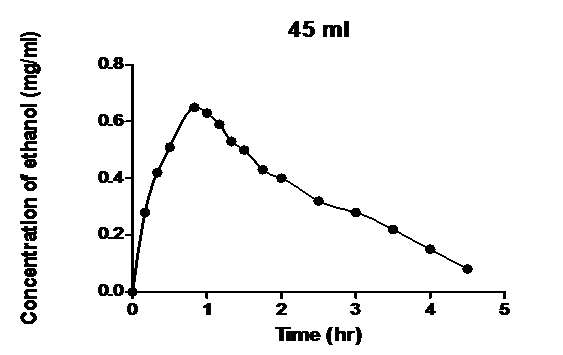
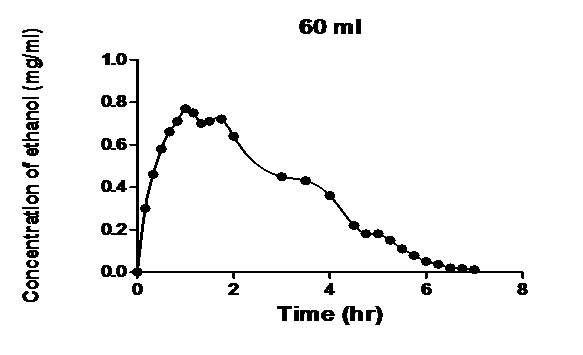
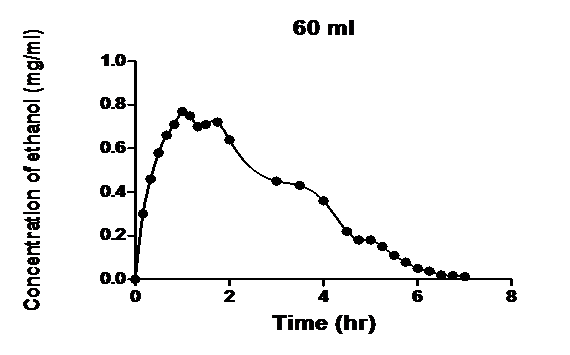
As seen in Figures 1 - 4, the mathematical models developed successfully described
Figure 1: Blood ethanol concentration-time profile measured after intravenous infusion of ethanol to dogs[1] and the model developed.
Figure 2: Blood ethanol concentration-time profile measured after intravenous infusion of ethanol to dogs[1] and the model developed.
Figure 3: Blood ethanol concentration-time profile measured after intravenous infusion of ethanol to dogs[1] and the model developed.
Figure 4: Blood ethanol concentration-time profile measured after intravenous infusion of ethanol to dogs[1] and the model developed.
References
- 1. Dedík, L., Ďurišová, M. Frequency response method in pharmacokinetics. (1994) J Pharmacokinet Biopharm 22(4): 293-307.
- 2. Wilkinson, P.K., Rheingold, J.L. Arterial-venous blood concentration gradients. (1981) J Pharmacokinet Biopharm 9(3): 239-387.
- 3. Hawkins, R.D., Kalant, H. The metabolism of ethanol and its metabolic effects. (1972) Pharmacol Rev 24(1): 67-157.
- 4. Finch, J.E., Kendall, M.J., Mitchard, M. An assessment of gastric emptying by breathalyzer. (1974) Br J Clin Pharmacol 1(3): 233-236.
- 5. Wsterfeld, W.W., Scgulman, M.P. Metabolism and caloric value of alcohol. (1959) J Am Med Assoc 170(2): 197-203.
- 6. Wagner, J.G., Wilkinson, P.K., Sakmar, E., et al. Elimination of alcohol from human blood. (1976) J Pharm Sci 65(1): 152-154.
- 7. Sedman, A.J., Wilkinson, P.K., Wagner, J.G. Concentrations of ethanol in two segments of the vascular system. (1976) J Foren Sci 21(2): 315-322.
- 8. Wilkinson, P.K., Sedman, A.J., Sakmar, E., et al. Pharmacokin etics of ethanol after oral administration in fasting state. (1977) J Pharmacokinet Biopharm 5(3): 207-224.
- 9. Levy, E.C. Complex curves fitting. (1959) IRE Trans on Automatic Control AC 19(1): 37-43.
Pubmed||Crossref||Others
- 10. Weiss, M., Pang, K.S. Dynamics of drug distribution. I Role of the second and third curve moments. (1992) Pharmacokinet Biopharm 20(3): 253-278.
- 11. Ďurišová, M., Dedík, L. Comparative study of human pentacaine in time and frequency domain. (1994) Methods Find Exp clin Pharmacol 16(3): 219-232.
- 12. Dedík, L., Ďurišová, M. CXT-a programme for analysis of linear dynamic systems in the frequency domain. (1995) Int J Biomed Comput 39(2): 231-241.
- 13. Ďurišová, M., Dedík, L., Balan, M. Building structured model of a complex pharmacokinetic system with time delays. (1995) Bull Math Biol 57(6): 787-808.
Pubmed||Crossref||others
- 14. Dedk, L., Ďurišová, M. CXT – a programme for analysis of linear dynamic systems in the frequency domain. (1995) Int J Biomed Comput 39(2): 231-241.
- 15. Dedík, L., Ďurišová, M. CXT-MAIN: a software package for determination of the analytical form of the pharmacokinetic system weighting function. (1996) Comput Methods Programs Biomed. 51(3): 183-192.
- 16. Dedík, L., Ďurišová, M. System approach to modeling metabolite formation from parent drug: a working example with methotrexate. (2002) Methods Find Exp Clin Pharmacol 2(8): 481-486.
Pubmed||Crossref||Others
- 17. Dedík, L., Ďurišová, M. System approach methods for modeling and testing similarity of in vitro dissolutions of drug dosage formulations. (2002) Comput Methods Programs Biomed 69(1): 49-55.
Pubmed||Crossref||Others
- 18. Ďurišová, M., Dedík, L. A system-method method for the adjustment of time-varying continuous drug infusion in individual patients: a simulation study. (2002) J Pharmacokinet Pharmacodyn 29(5-6): 427-444.
- 19. Ďurišová, M., Dedík, L. New mathematical models in pharmacokinetic modeling. (2005) Basic Clin Pharmacol Toxicol 96(5): 335-342.
- 20. Ďurišová, M., Dedík, L., Kristová, V., et al. Mathematical model indicates nonlinearity of noradrenaline effect on rat renal artery. (2008) Physiol Res 57(5): 785-788.
Pubmed | Crossref||Others
- 21. Dedík, L., Tvrdoňová, M., Penesová, A.,et al. Computer controlled sequential simulation method: reconsidering evaluation of measurements from sampled intravenous glucose tolerance test. (2009) Comput. Methods Programs Biomed 95(1): 1-9.
- 22. Ďurišová, M. Physiologically based structure of mean residence time. (2012) Scientific World Journal: 4.
- 23. Ďurišová M. A physiological view of mean residence times. (2014) Gen Physiol Biophys 33(1): 75–80.
- 24. Ďurišová, M. Mathematical model of pharmacokinetic behavior of orally administered prednisolone in healthy volunteers. (2014) J Pharmaceut Pharmacol 2(2): 1-5.
Pubmed||Crossref||Others
- 25. Ďurišová, M. Another example of a successful use of computational and modeling tools from the theory of dynamic systems in pharmacokinetic modeling. (2015) J Pharmacut Pharmacol 3(1): 1-3.
Pubmed||crossref||Others
- 26. Ďurišová, M. Mathematical model of the pharmacokinetic behavior of theophylline. (2016) Ec Pharmacol Toxicol 2(4): 156-164.
Pubmed||Crossref||Others
- 27. Beckmann, B., Kaliaguibe, V. The diagonal of the Padé table and the approximation of the Weyl function of second order difference operators. (1997) 13(4): 4 81-510.
- 28. Verotta, D. Fractional dynamics pharmacokinetics-pharmacodynamic models. (2010) J Pharmacokinet Pharmacodyn 37(3): 257-276.
- 29. Akaike, H. A new look at the statistical model identification. (1974) IEEE Trans Automat control 19(6): 716-723.
Pubmed||Crossref||Others
- 30. Argyros, I.K., Hilout, S. On the Gauss-Newton method. (2011) J Appl Math Comput 35(1): 537-550.
Pubmed||Crossref||Others
- 31. Elishakof, F.I. Notes on philosophy of Monte-Carlo Method. (2003) J Int Appl Mech 39(7): 753-762.
Pubmed||Crossref||Others
- 32. Siegel, R.A. Pharmacokinetic transfer functions and generalized clearances. (1986) J Pharmacokinet Pharmacodyn 14(5) 511-521.
- 33. Wagner, G.J. A modern view of pharmacokinetics. (1973) J Pharmacokinet Biopharm 1(5): 363-401.
- 34. Smolen, V.F. A frequency response method for pharmacokinetic model identification. (1981) In: L. Endrenyi (ed): 209-233.
Pubmed||Crossref||Others
- 35. Segre, G. The sojourn time and its prospective use in pharmacology. (1988) J Pharmacokinet Biopharm 16(6): 657-666.
- 36. Derr, R.F. Simulation Studies on ethanol metabolism in different human populations with physiological pharmacokinetic model. (1993) J Pharm Sci 82(7): 677-682.
- 37. Umulis, D.M., Gürmen, N.M., Singh, P., A physiologically based model for ethanol and acetaldehyde metabolism in human beings. (2005) Alcohol 35(1): 3-12.
- 38. Seidl, S., Jensen, U., Alt, A., The calculation of blood ethanol concentrations in males and females. (2000) 114(1-2): 71-77.