InfoGenomics Tools: A Computational Suite for Informational Analysis of Genomes
Vincenzo Bonnici,Vincenzo Manca*
Affiliation
Department of Computer Science, University of Verona, Strada le Grazie, Verona, Italy.
Corresponding Author
Vincenzo Manca . Department of Computer Science, University of Verona, Italy. E-mail: vincenzo.manca@univr.it
Citation
Manca, V., et al. Infogenomics Tools: A Computational Suite for Informational Analyses of Genomes. (2015) Bioinfo Proteom Img Anal 1(1): 7- 14.
Copy rights
©2015 Manca, V. This is an Open access article distributed under the terms of Creative Commons Attribution 4.0 International License.
Abstract
Infogenomics is a project aimed at developing informational analyses of genomes adding a new perspective to the more common biological and biochemical investigation on genomes. Here, we present InfoGenomics Tools, shortly IGTools, a computational framework, which consists of a collection of interactive tools, designed to support typical analyses re- quired in the context of Infogenomics. Modularity, interactiveness, data visualization, and low-cost computational requirements are the main goal of IGTools, where suffix arrays are a key point in the data structures representing genomes, and their algorithmic power allows us to speed-up genomic computations that would be prohibitive by using naive methods.
Introduction
Nowadays, the genomes of hundreds of species have been sequenced, from bacteria to vertebrate kingdoms[1,2], and a huge amount of genomic information is available. The Human Genome Project[3] and the sequencing of thousands whole human genomes, such as those affected by rare disease[4], provide an invaluable source of knowledge. However, a deep understanding of the internal organization of genomes and of their specific languages is so far missing.
Recently, a project, called ENCODE[5,6], involved several scientists and laboratories around the world and provided evidence that 80% of the human genome, previously considered junk regions, is covered by functional elements. ENCODE created an encyclopaedia of DNA elements by annotating portions of the human genome in terms of their biochemical function.
On the other side, the Infogenomics project[7-9] aims at proving an analogous annotation, but in terms of informational concepts, by extracting genomic fragments, or genomic words, on the basis of their relevance, according to the information theory. To this end, genomes are investigated by means of genomic distributions, genomic dictionaries, informational indexes, and genomic representations.
In the last decades, bioinformatics approaches, regarding sequence analysis, were mainly focused on methodologies based on string alignment algorithms. However, even if they have been used to extract plenty of biological results, such approaches appear to be not suitable to discover genomic aspects of systemic nature. An alternative perspective[10-12] is based on alignment-free methods of genome analysis, where global properties of genomes are investigated.
A key concept of the informational perspectives in genome analysis is thatof genomic distribution. A genomic distribution associates to the discrete values assumed by a given a quantity, defined on genomes, the number of times these values occur in a given genome. The general concept of discrete probability distribution, called information source, was the starting point of the Information theory developed by Shannon[13].
Links between information theory and biology are well established, continuously remerging, and deeply rooted (Shannon’s Ph.D. thesis, titled ‘An Algebra for Theoretical Genetics’ (1940), precedes his famous booklet where he notion of information entropy was introduced)[14-16].
For example, distributions of codons have shown that protein encoding regions own a characteristic property, called 3-peak regularity[17-19], which is absent in other parts of a genome. This regularity is often taken into account by gene recognition algorithms[20]. More in general, informational analysis helps to highlight periodicities in DNA sequences which are linked to biological meanings, such as nucleosomal packaging and chromatin DNA pitch[21,22]. Other approaches based on the recurrence of genomic elements and on the study of correlation structures in DNA sequences[23] use mutual information, which plays a central role in the mathematical analysis of message transmission.
The recurrence distance distribution (RDD)[24,25] takes into account the distances at which a given k-mer recurs, and, for each recurrence distance, it specifies the number of time that the k-mer recurs at such distance. This distribution helps to highlight important features of genomic elements[26], and can be used to identify and capture recurrence properties of “genomic words”[27,28].
Dictionary based methodologies (such as [29-32]), aim at analysing genomic sequences through properties of collections of genomic words (dictionaries).
In general, software libraries are developed in order to hide low-level aspects regarding algorithmic knowledge or data representation. In this way, users who operate at higher level of abstraction, and who require ready-to-use black boxes, can be unaware of implementation details of basic components used in their analysis. For example, the LEDA library[33] provides algorithms and efficient data structures in the field of graph theory and computational geometry. In Natural Language Processing (NLP), the Stanford CoreNLP toolkit[34] is an extensible pipeline, developed in Java, which provides most of the common core procedures used in the NLP field. In bioinformatics, several frameworks have been developed in order to provide easy-to-use implementation of the most used algorithms and data structures, such as sequence alignment algorithms or sequence indices based on suffix arrays and q-grams.
The SeqAn[35] library is an extensible C++ library that provides basis algorithms and data structures used in bioinformatics, such as binary representation of biological sequences, alignment algorithms and sequence indices (suffix arrays, q-gram approaches, and FM Index). However, none of the data structure is equipped with dictionary operations (such as k-mer enumeration). The BioPerl tool kit[36] provides a collection of Perl modules for managing and manipulating sequences analysis pipelines. Both SeqAn and BioPerl do not provide interactive graphical interfaces. The BioJava project[37] provides a bioinformatics framework mainly focused on biological sequence alignment and protein structure analysis. The Bio-Conductor framework[38] is an extension to the R environment which aims at providing a deployment environment in order to facilitate computational analysis of high-throughput data. More than one thousand packages have been developed on top of it that are mainly focused on statistical analysis.
Here, we present a computational framework to support informational analysis typical of Infogenomics. Namely, a suite of interactive tools is mainly designed for extraction of k-dictionaries, set-theoretic operations on them, their visualization, as well as charts of distributions defined on k-mers and k-dictionaries, and computations of indexes defined on these distributions. Section 2 gives some preliminaries regarding genomic sequences and informational analyses taken into account by Infogenomics and state-of-art methodologies for string processing. The IGTools environment is introduced in section 3, where the main goals and the principal aspects of the project are described. Section 3.1 describes the core data structure of the framework, by which basic dictionary operations are implemented. Sections 3.2 and 3.3 focus on graphical IGTools, by showing a selection of them. Conclusions and future works are given in the final section of the paper.
Preliminaries
Basic notation and concepts of Infogenomics are given below. More details can be found in[8]. A DNA sequence is abstractly a string over the nucleotide alphabet Γ = {A, C, G, T}. The extended alphabet Γ≅ {A, C, G, T, N}, adds to Γ symbol N that represents an undefined nucleotide. Γk denotes the set of words of length k, called k-mers, including the empty string λ, and Γ+ denotes the set of all the possible non empty string over the alphabet Γ. Given a genomic string S = a1 • a2 • • • • • an, of length n, S[i, j] : 1 ≤ i ≤ j ≤ n is the substring of S from position i to position j (included), while S[i] = S[i, i] is the symbol in position i of S. If n is the length of S, that is, S = S[1]S[2] ... S[n], then we write |S| = n, and S[1, j] : 1 ≤ j ≤ n is called a prefix of S and S[i,n]: 1 ≤ i ≤ n, is called a suffix of S. Substrings of S of type S[i, j] : i ≤ j ≤ n of length k are also called k-words, k -factors, k-mers of S (k may be omitted, when it is not relevant, or it may be assumed as a generic integer). In the following, entire genomes are denoted by letter G (possibly decorated). For a finite set A, then |A| denotes its cardinality, and for a finite multiset X (where elements may occur in many copies), then |X| denotes its size, that is, the sum of the multiplicities of elements occurring in X.
Given a word α, we identify with posS(α) the set of (initial) positions where α occurs in the string S and with multS(α) = |posS(α)| the multiplicity of α in S. A word α with multiplicity equal to 1 is called hapax (of S), otherwise it is called repeat. The set of all factors of S, of any length, is denoted with D(S), while the set of k-factors, for a specific value of k, is denoted with Dk(S).We remark that |D (S)| = (|S| × |S| + 1)/2.
Starting from Dk(S), we define the k-genomic table Tk(S) by equipping the words in Dk(S) with their multiplicities, thus Tk(S), mathematically corresponds to a multiset, or to a discrete distribution, which can be represented with a list of associations α → multS (α), for α ∈ Dk(S). The set of hapaxes of length k that occur in S is denoted by Hk(S), and the set of repeats of length k is denote by Rk(S). Many important indexes can be defined on genomes, related to characteristics of genome dictionaries. For example, mrl(G) is the length of the longest repeats of G. Of course mrl(G), is the minimum length, such that k-mers with k greater than mrl(G) are all hapaxes. Analogously, mhl(G) is the length of the shortest hapaxes of G, and of course, k-mers with k smaller than mhl(G) + 1 are all repeat. The index mfl(G) denotes the length such that all possible k-mers with k smaller than mfl(G) (maximal forbidden length) are included in D(G). These indexes are very important in many aspects of analysis of genomes. We mention them just for a better outline of infogenomics approach, even if their importance and use is beyond the aims of the present paper.
Enhanced suffix array
The suffix tree is one of the most important data structure in string processing. It can be used to solve a myriad of problems in string processing such as substring searching or string regularities extraction[39]. Unfortunately, its space consumption represents a limit in its application, especially in the field of computational genomics. A compact representation of suffix trees can be obtained by combining different data structures. In[40], suffix arrays (SA) and the longest common prefix (LCP) array are combined together to provide a data structure, called enhanced suffix array, which is equivalent to suffix trees.. Both SA and LCP arrays can be built in linear time, and are able to be extended with additional features. Enhanced suffix array are an extension of SA that provide a methodology for substring search in optimal time. Given a string S over an ordered alphabet, its suffix array, SAS, is an array of positions of S having the same length of S, where SAS [i] identifies the starting position of the i-th suffix of S in the lexicographic order, while LCPS [i] for i 1 is the length of the longest common prefix between the suffix SAS [i] and the suffix SAS [i − 1] (LCPS[1] is set to 0). A k-interval of LCPS is a contiguous range [i, j] of positions in LCPS such that:
LCPS [i] < k, LCPS [l] ≥ k for i< l ≤ j and LCPS [j + 1] < k.
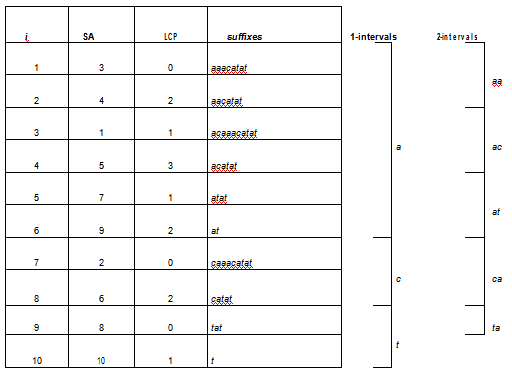
Suffixes belonging to the same k-interval, for some positive integer k, share the same k-prefix, also called the prefix of that k-interval. Therefore, given a k-mer α that is prefix of some k-interval [i, j] of SAS, the positions of α in S are all and only those belonging to SAS[i, j]. Figure 1, shows a toy example of the enhanced suffix array for the string acaaacatat. The column i represents the arrays positions while the column suffixes shows the suffixes starting from SAS[i]. Both i and suffixes columns are not stored inside the data structure. Once SA is built, suffixes[i] can be retrieved by looking at position SAS[i] of S. Thus, the memory requirement of a complete enhanced suffix array is given by the space needed to store SA and LCP arrays plus the space to represent the sequence. Given the SA and LCP arrays, suffix tress can be efficiently simulated to support substring querying. Moreover, with the addition of LCP-intervals, SA can be used to enumerate the k-mers of S in lexicographic order. An example of their application to retrieve k-mer frequencies in genomic sequences is given in[41].
Figure 1: Enhanced suffix array for the string acaaacatat. The gure also depicts the k-intervals of 1-mers and 2-mers contained in the given string, and retrieved by means of the LCP array.
InfoGenomics Tools
The main aim of the IG Tools is to help the researcher to investigate genomes, from an informational point of view, by means of a set of interactive software packages having low computational requirements and that could be executed on domestic computers. Thanks to this capability, the researcher can focus onto the main stream of the analysis process, gaining time and focusing on reading and interpreting data. For example, multiplicity analysis over several values of k is done instantly. Extraction of dictionaries, and their representations and visualizations correspond to main IGTools functionalities. These can be directly applied to the simple case of Dk(G), or to more complex cases of word selections, according to specific constraints (coverage, elongation, anti-random properties) that can be realized by combining basic functionalities within more complex procedures. Moreover, basic genomic distributions and their visualization (for example, recurrence distance distributions) can be performed by means of IG Tools with low computational costs, and genome indexes evaluation over genomes, dictionaries and distributions can be directly computed.
IGTools core library supplies genome representations with their corresponding suffix arrays[41,42], which are well-established data structures, here adapted to genomic sequences. Moreover, the extended suite includes Graphical user interfaces (GUI) and command-line interfaces (CLI). CLIs are suitable for batch and/or extensive computations, while GUIs provide an interactive interface for investigative analyses.
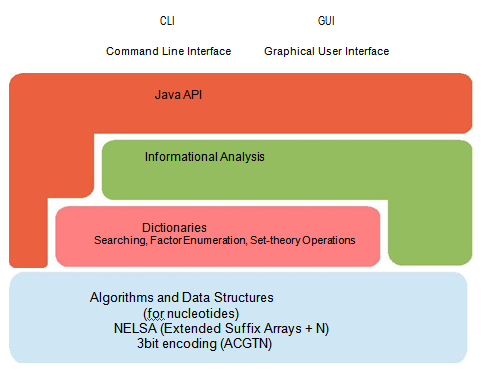
A collection of API for developers is provided, which is easy to use and to extend for custom analyses. APIs provide access to all the abstraction levels of the framework (Figure 2). The lowest level implements the core data structures and algorithms (enhanced suffix arrays[40], and succinct nucleotide sequence representation). The middle level implements typical operations for dictionary construction and for the realization of basic elaborations over dictionaries (words enumeration, localization, multiplicity count, elongation, as well as set-theoretic operations among dictionaries). Finally, the highest level implements the typical informational analyses defined in Info genomics, such as the computation of genomic distributions, their analysis and manipulation.
Figure 2: Abstraction layers and functionalities of the IGTools platform.
An important aim of the IGTools is to facilitate the different types of users involved in genome analyses. It is an open source resource such that developers can investigate, modify and extend it with new core functionalities. They can also combine the already implemented functionalities within their own software thanks to the library APIs. Graphical and command-line interfaces are intended to be used by users who have not programming skills, but want to apply to specific genomes one the informational analyses available in the IGTools environment. Table 1 reports the main functionalities offered by IGTools and the level at which they are available to be used. For example, the dictionary size distribution, that reports the cardinalitiesof Dk(G) for a given range of values of k, is computed by a procedure accessible via the core framework API, it can be retrieved by making use of a CLI tool, and it can be visualized and investigated with a tool included in the graphical interface. Beside informational analyses, the CLI suite includes a set of tools in order to deal with variable length dictionaries, namely set of words in FASTA format provided by the user. CLI tools are developed such that their output can be easily parsed (i.e. extract a textual tabular file such as CSV files). GUI tools are accessible via a unified interface depicted in Figure 3.
Table 1: List of the main functionalities provided by IGTools. The table reports the level at which a functionality is made available. The user is referred to[7,8,9] for the complete terminology.
| API | CLI | GUI | |
| Genomic Indexes | |||
| jDk(G)j; jRk(G)j, and jHk(G)j | X | X | |
| mrl, mhl, k-completeness, k-entropy, k-lexicality | X | X | X |
| min, max, average and SD of multiplicities in Tk(G) | X | X | X |
| Genomic Distributions | |||
| Dictionary size distribution | X | X | X |
| Multiplicity-CoMultiplicity | X | X | X |
| k-mer multiplicities | X | X | X |
| Parikh vector distributions | X | X | X |
| RDD (minimal, non-minimal, self and pair recurrences) | |||
| extraction | X | X | X |
| navigation within RDDs of Dk(G) | |||
| extraction of enclosed sequences | X | X | |
| Peak 3-regularity [19] analysis by means of RDD | X | X | |
| Multiplicity Heat maps | X | X | X |
| Expon. And Geom. Distribution Estimation | X | X | X |
| Metrics: average value, SD, skewness, Kurtosis, percentiles | X | X | |
| Divergences (KL [43], KS [44] , sum of differences) | X | X | |
| Peak recognition | X | X | |
| Genomic Representation (and visualization) | |||
| Visualization of G | X | ||
| Visualization of Dk(G) | X | ||
| Dictionary operations | |||
| Set-theoretic operations on Dk(G) | X | X | |
| Variable-length dictionaries | |||
| Set-theoretic operations | X | ||
| Shared prefixes | X | ||
| Duplicate removal | X | ||
| Relevant genomic distributions | X | ||
| Statistics with respects to G | X | ||
| H(D; G); R(D; G); MH(D; G); and MR(D; G) | X | ||
| coverage | X | ||
| coverage by word length | X | ||
| Parikh vector Coverage | X | ||
| multiplicity-comultiplicity distribution | X | ||
| Other kind of analyses | |||
| Random genome generation | X | X | |
| Clustering coecients [45, 26] | X | X | |
| Unique G factorization algorithms [30] | X | X | |
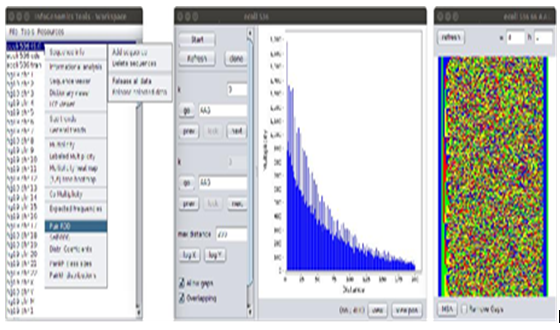
Figure 3: A usage example of the GUI interface of IGTools. In the left side, the gure show the main window of the GUI, which serves as entry point to the set of graphical analyses that can be performed on genomic sequences. The main window visualizes a list of sequences that ave been previously uploaded (even in previous working sessions) by the user. Sequences can be uploaded or removed from the workspace via the Resources menu. Their representations (sequence and indexing structures) are loaded in main memory on demand, when an analysis has to be performed on then, and they can be explicitly released by the user in order to gain memory resources. In the proposed example, the tool for RDD distributions of pair-recurrences have been selected from the Tools menu. It is depicted by the window shown in the central part of the gure. Then, the recurrence distance 66 have been selected by clicking on the corresponding bar of the distribution chart. After the recurrence distance selection, the set of sequences enclosed between occurrences of the word AAG at distance 66 is shown in a separate window (right side) by making use of the technique described in Section 3.3.
The software is entirely developed in Java, using the OOP (Object-oriented programming) paradigm. The GUI side is implemented by using the standard framework JFC/SWING. An external library, called JFree Chart, is used to visualize classical widely used charts, and in-house components were developed to support further efficient data visualizations. The choice of Java is due to the different types of users that IG Tools wants to serve. A similar framework is SeqAn but it is developed in C++, this programming language requires advanced programming skills, and it results more difficult to develop graphical user interfaces[43].
NELSA: An Extended Data Structure
The basis of informational analyses over genomes are set operations over genomic dictionaries. The k-mer enumeration operation of IG Tools lists all the words of a specified lengthwith are owned by a genomic sequences, namely it serves to retrieve the Dk(G) dictionary of a given sequence G. Besides word enumeration, one may also want to directly access to word properties by a searching operation. Then, for each word of a dictionary of G, it is desirable to retrieve the number of times that it occurs, as well as the positions of its occurrences within the considered genome. With multiplicity information, which can be easily translated in terms of frequency, we can discriminate between hapaxes and repeats, and perform distributional analyses based on word multiplicity. With data regarding the positions of words, we can perform positional analyses, such as recurrence distances and biological annotation.
In the following, we first introduce the biological sequence representations used in IG Tools, then we show the core data structure NELSA and how informational operations can be performed on top of it[44].
IG Tools provides two main approaches for succinct genomic sequence representation. The first ideally considers a DNA sequence as a string over the alphabet Γ, and the lexicographic order in the nucleotide alphabet is assumed to be A < C < G < T. The symbols A, C, G, T are classically represented by the 2-bits encoding 00, 01, 10, 11, respectively. Then, the above encoding is extended to a 3-bits schema where the symbol N is represented by 100 and a zero is prefixed to the 2-bit encoding of the other symbols. Both types of encoding maintains the original lexicographic order (in 3-bits encoding N is consider as the last symbol of the alphabet) and the complementation property between nucleotides.
Some exiting libraries use only 2-bits encoding and they are not suitable to dial with real genomic sequences where undefined nucleotides are present. In dictionaries based approaches we are not interested in analyzing words which contains the symbol N, and we want to be able to discard them during basics operations, such as k-mer enumeration. Exiting approaches that use 3-bits encoding usually implements algorithms that discard N during search operations.
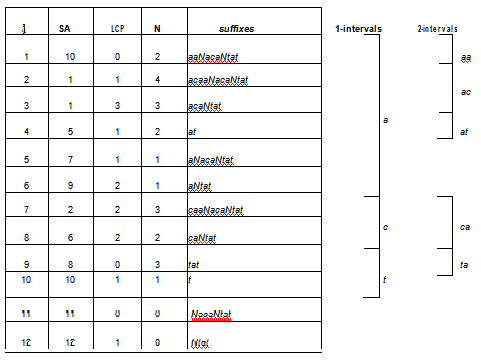
In IGTools N symbols are not eliminated but elaborated in a proper way. For example, enhanced suffix array have a further column to discriminate positions of SAS where symbol N occurs. Namely, starting from SAS we computed the array NS where NS[i] is 0 if S[SAS[i]] = N, otherwise it equals the distance between SAS[i] and the position of the next symbol N in S. It can be shown that NS can be built in linear time. Moreover, we modify the notion of k-interval, given in section 2.1, by adding the constraint NS[l] > k for i ≤ l ≤ j. We call this new data structure NELSA (N-array Extended LCP-SA). Figure 4 shows the content of the NELSA structure built for a string that includes symbols of type N.
Figure 4: The NELSA data structure for the string acaaNacaNtat. k-intervals are retrieved by taking into account both the LCP and the N arrays such that k-mers containing the symbol N are discarded.
With the introduction of the N array, we are able to perform k-mer enumeration over the alphabet Γ in order to extract genomic dictionaries and genomic tables. The k-interval of a word is also used to obtain the multiplicity and the positions at which the word occurs. Recurrence distances can be calculated by extracting and sorting the positions. Besides word-specific properties, the NELSA structure can be also used to extract global informational features of the analysed sequence. For example, the maximum repeat length of a genome gives the length of the longest repeat contained in the genome. A brute force procedure could scan over the dictionaries Dk(G) for several values of k until the wanted element is found. Instead, thanks to the NELSA structure, this operation can be performed efficiently. In fact, the searched length corresponds to the maximum value contained in the LCP array (if no symbols N are contained in the sequence) hat it is greater to the corresponding value in the N array.
The more data we include in the data structure, the higher is the memory requirement and this can turns in unaffordable costs if, for example, one needs to compare several sequences. However, the suffix order, with which the NELSA is built, allows us to enumerate k-mers in their lexicographic order sequentially, by making use of relatively small parts of the data structure. Usually, the higher is k the smaller are the k-intervals. In order to implement set-theoretic dictionary operations for long sequences we can use two different strategies. For low values of k, we use small tables where each position identify a k-mer in Γk. Instead, for high values of k, we can use a disk based NELSA version through which data related to each k-mer are loaded once a time. A useful example is given by dictionary intersections. Let us to image to intersect the k-dictionaries of two long sequences, S1 and S2, such that their NELSA cannot be loaded simultaneously in the primary memory. We can built their NELSA separately, save them on the disk, and perform their intersection using the following strategy. Genomic sequences arerepresented in a succinct way thanks to the 3-bits encoding, thus they can be loaded in primary memory. Data, in SA, LCP and N arrays, corresponding to a given position i, are consecutively stored inside the NELSA file. The intersection operation can be performed by sequentially comparing k-intervals and the k-mers associated to them. In this way, just one k-interval per sequence needs to be loaded in memory. Thanks to this technique, we were able to enumerate all the 144,405 words, coming from the intersection of the D30dictionaries of all human chromosomes, in just 2,121 seconds.
K-mer Multiplicity
In this section we show some of the graphical tools provided by the IGTools suite which regard the notion of word multiplicity.
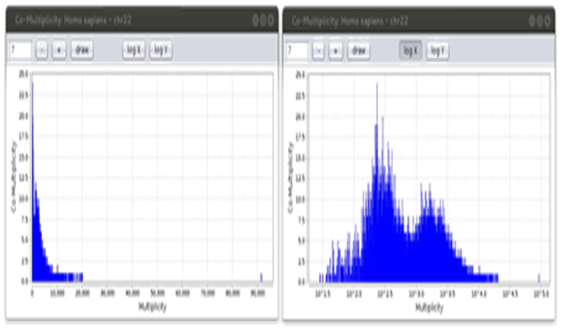
In[7], it is shown that biological species hold specific Zipf curves and multiplicity-comultiplicity (the number of words having a given multiplicity) bar charts. Thanks to IGTools, it is possible to quickly navigate among charts, obtained at different values of k, and investigate new features. For example, Figure 5 shows the multimodal behaviour in the multiplicity-co multiplicity chart of human chromosome 22, highlighted applying a logarithmic scale to the x-axis.
Figure 5: Multiplicity-comultiplicity chart of human chromosome 22 for k = 7. The right side of the image shows the chart by applying a logarithmic scale to the x-axis. In this way, the two modes of the distribution appear more clearly.
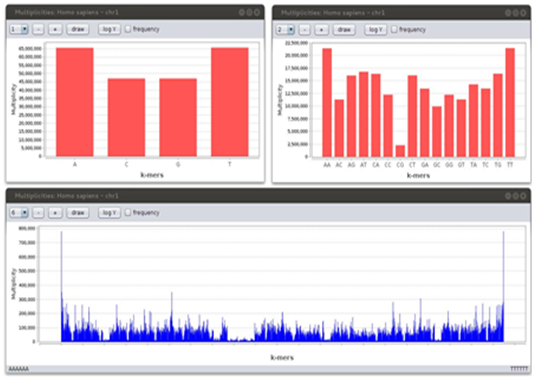
A bar chart to plot k-mer multiplicities is often useful Figure 6. On the x-axis, k-mers in Γk are represented in their lexicographic order and their multiplicity is plotted via bars. Of course, for low values of k, this type of visualization does not involve special efforts, but for relatively high values IGTools has clear advantages. In fact, an interactive interface (provided by JFree Chart) helps to navigate (i.e. by zooming) the data, especially when a huge amount of information is shown.
Figure 6: K-mer multiplicity charts of human chromosome 1 for k = 1 (upper left), 2 (upper right) and 6 (bottom).
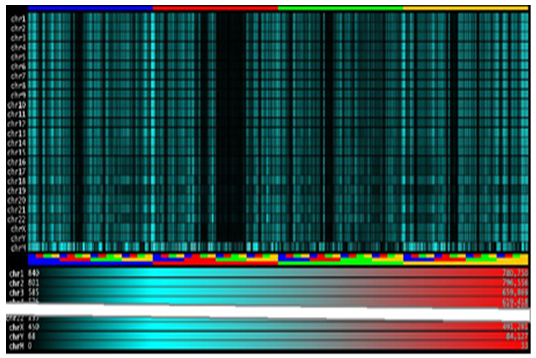
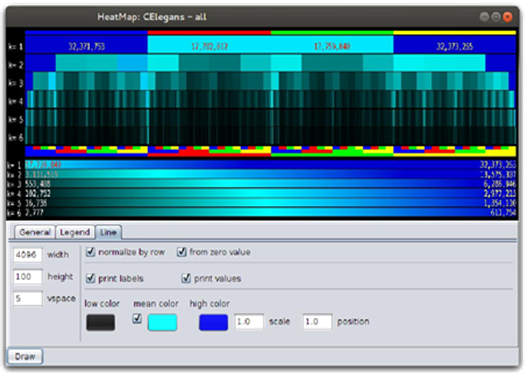
Multiplicities charts can be used for a visual comparison of genomes, but when several sequences are involved a more compact representation is needed. For this reason, IGTools uses a visualization via heat maps. This kind of graphical representation is created by filling regions of a two-dimensional image with specific colors. Each region of the image identifies a specific k-mer and its multiplicity is represented by a color chosen from a gradient palette. The IGTools suite provides specialized components to create heat maps and to set their parameters. In Figure 7, heat maps of 6-mer multiplicities coming from human chromosomes are plotted together. Each row identifies a specific chromosome and k-mers are plotted in their lexicographic order, from left to right, by a 1 × 100 pixels shape. Colors are chosen according to a mapping between the multiplicity and the desired gradient palette. A multiplicity equal to zero is mapped to black, while the maximum multiplicity (inside a single chromosome) is mapped to red. In the bottom side, a legend indicates the minimum and maximum multiplicity in each chromosome and how their map to colors. Like for the previous chart type, we can easily relate a specific area of the image to the corresponding k-mer thanks to the lexicographic order in which k-mers are plotted. In figure, it appears clear that human chromosomes share a common 6-genomic table except for the mitochondrial one.
Figure 7: Multiplicity heat maps of all human chromosomes. The colour gradient is mapped in the range [0; max α∈Dk(S) multS(α)] of each chromosome.
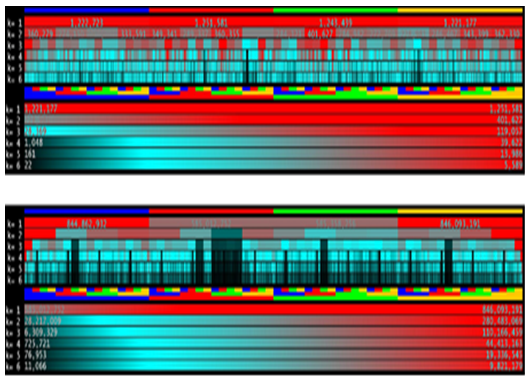
Multiplicities, presence ad absence of k-mers in a sequence are directly related to the multiplicity of their factors. Heat maps can also be useful to compare dictionaries obtained at different values of k. Figure 8 shows heat maps, for k in[1-6] interval, of human chromosome 22. An example analysis, that can be done using this visualization, is the direct correlation between the low multiplicity of 2-mer CG and the multiplicity of longer k-mers having CG as factor. Moreover, like for previous visual analyses, each biological species hold a specific resultant heat map as it appears in the figure. There are plenty of parameters that can be chosen in building the overall image. The most important ones regard the construction of the color gradient and how values are mapped to it. They may sensibly affect the legibility of reported data. Thus, every graphical tools is equipped with one more control panels which allow the user to fully customize the output images. Figure 9 shows tools for constructing the heat map discussed above. Via the control panel, it is possible to choose the palette colors, which may results useful to color-blind users, and set other layout parameters such as font size and spaces between the rows in the image.
Figure 8: k-mer multiplicity heat map of Escherichia coli (top) and Homo sapiens (bottom). Values of k are (1, 2, 3, 4, 5, 6) and displayed in the same order, from top to bottom. Multiplicities are normalized in the range [0, max α∈Dk(S) multS(α)].
Figure 9: The graphical component of IGTools to generate heat maps
Dictionary Visualization
In this section we introduce some techniques to visualize DNA sequences and genomic dictionaries. The visualization of DNA sequences, or DNA k-mers, is based on a mapping between Γ~ and a predefined color palette. Color combinations and color perception are well studied topics physiology and computer graphics. In electronic systems, a well-established color model is the RGB one (Red, Green and Blue), formed by the three primary additive colors. In the human eye’s retina there exist three kind of photoreceptor cells responsible for color vision. They are distinguished according to the color to which they are sensitive, specifically red, green and blue. They function best in relatively bright light, as opposed to rod (rhodopsin) cells that work better in dim light. Rod cells have peak sensitivity to blue-green light, which can be approximate to yellow. Thus, the color palette that we use to visualize nucleobases is formed by the four colors mentioned above. This allows a visual uniformly perception among the nucleotides. We also admit a special color for undefined nucleotides (N). The color palette is mapped to Γ~ by the following schema:(A → blue), (C → red), (G → green), (T → yellow) and (N → gray). Besidesthe proposed colorschema, every tools that make use of it also allows the user to choose a customized palette by the tool’s control panel, this feature may result useful in case of daltonian users.
Thanks to the above schema, dictionaries and their elements can be presented in a visual way. K-mers in Dk(S) are displayed from top to bottom, according to their lexicographic order. In the image, each row represents a single k-mer printed from left to right using the colorscheme. An example of such representation is given in Figure 10 where 300 50-mers sharing a poly-AAG prefix are show. Due to the lexicographic order in which k-mer are plotted, the image results in a contiguous blue green area on the left side. Multiplicities can be plotted nearby k-mer lines as shown in the figure. In this case, the multiplicity chart is vertically arranged, since it follows the k-mers orientation, and values are logarithmically scaled. Due to the limited space, a special chart accompanies the multiplicity one to identify hapaxes (displayed with a red segment) and k-mers having multiplicity less than 11 (blue segments). Moreover, two further visualization parameters can be set. The first one still regards multiplicities and consists in changing dynamically the shape with which k-mer nucleotides are plotted, in such a way that the height equals the k-mer multiplicity. The second one does not reshape the polymer representation but plots the k-mer and itsfollowing nucleotides in the sequence (looking at its position in G) up to the LCP value. Figure 10 shows several plots obtained by combining visualization parameters. When the NELSA is loaded in primary memory, the viewer tool allows to navigate in real-time along the dictionary by mouse scrolling or keyboard keys. Displaying genomic dictionaries by graphical representation allows to visualize local details and, combined with globaldetails (such as multiplicity chats shown in the previous section), gives a better understanding of their phenomena. These features appear more evident on increasing k, when dictionaries became very large and present a lot of missing words[45].
Figure 10: Partial plots of the same D50 dictionary (of human chromosome 22) region, visualized using di erent parameter settings. K-mers are represented with shapes of size 4x1 and plotted in western writing style. (a) is a simple visualization. In (b) multiplicity bars are shown as well as in (c) and (d). K-mer shapes are stretched according to multiplicity, in (c) and (d). In (d), words are extended up to the LCP value.
Conclusion
In this paper we presented the general ideas behind the IGTools suite, developed in the context of the Infogenomics project. The main aim of this software concerns with the extraction of informational regularities. The results, obtained from this kind of analyses, could be useful to integrate biochemical and biological annotations with informational annotations. Here, only some preliminary functionalities were considered. More complex genomic analyses are under development, which are grounded on specific aspects of statistical and informational properties of dictionaries. In this context empirical entropies (easily computable by IGTools), several kinds of entropic divergences (and their specializations to genomes), and random genomes are crucial notions for the extraction of genomic dictionaries where words are selected by means of sophisticated informational filters, and their relations and categories can be shed new light in the complex structure of real genomes.
References
- 1. Pagani, I.,Liolios, K.,Jansson, J.,et al. The genomes online database (gold) v.4: status of genomic and metagenomic projects and their associated metadata. (2012) Nucleic Acids Res 40(D1): D571- 579.
- 2. Koepfli, K.P., Paten, B., O'Brien, S. J. The genome 10k project: A way forward. (2015) Annu Rev Anim Biosci 3: 57- 111.
- 3. Craig Venter, J., Adams, M. D., Myers, E. W., et al. The sequence of the human genome. (2001) Science 291(5507): 1304- 1351
- 4. 1000 Genomes Project Consortium, Abecasis, G.R., Altshuler, D., et al. A map of human genome variation from population-scale sequencing. (2010) Nature 467(7319): 1061- 1073.
- 5. Feingold,E.A., Good, P.J., Guyer, M.S., etal. The ENCODE(ENCyclopedia of DNA elements)Project. (2004) Science 306(5696): 636- 640.
- 6. Dunham, I., Aldred, S. F., Collins, P. J., et al. An integrated encyclopedia of DNA elements in the human genome. (2012) Nature 489(7414): 57- 74.
- 7. Castellini, A., Franco, G.,Manca, V. A dictionary based informational genome analysis. (2012) BMC Genomics 13: 485.
- 8. Manca. V. Infobiotics: information in biotic systems (2013) Springer
- 9. Franco, G., Milanese, A. An Investigation on Genomic Re-peats. The Nature of Computation. Logic, Algorithms, Applications. (2013) Springer pages 7921: 149- 160.
- 10. Hao,B., Qi, J.Prokaryote phylogeny without sequence alignment: from avoidance signature to composition distance. (2004) Proc IEEE Comput Soc Bioinfo Conf 2: 375- 84.
- 11. Vinga, S., Almeida, J.Alignment-free sequence comparison|a review. (2003) Bioinformatics 19(4): 513- 523.
- 12. Yin, C., Chen, Y., Yau, S. S., et al.A measure of DNA sequence similarity by fourier transform with applications on hierarchical clustering. (2014) J Theor Biol 359: 18- 28.
- 13. Shannon, C. E.A Mathematical Theory of Communication. (1948) Bell LabsTechnical Journal 27(3): 379- 423.
- 14. Gatlin, L.L.The information content of DNA.(1966) J Theor Biol 10(2): 281- 300.
- 15. Gatlin, L. L. Information theory and the living system. 1972
- 16. Vinga, S. Information theory applications for biological sequence analysis. (2013) Brief bioinform 15(3): 376- 389
- 17. Fickett, J. W.Recognition of protein coding regions in DNA sequences. (1982) Nucleic Acids Res 10(17): 5303- 5318.
- 18. Shepherd, J. C.W. Periodic correlations in DNA sequences and evidence suggesting their evolutionary origin in a comma-less genetic code. (1981) J Mol Evol 17(2): 94- 102.
- 19. Eigen,M., Winkler-Oswatitsch,R. Transfer-RNA, an early gene? (1981) Naturwissenschaften 68(6): 282- 292.
- 20. Marhon, S.A., Kremer, S.C. Gene prediction based on DNA spectral analysis: a literature review. (2011) J Comput Biol 18(4): 639- 676.
- 21. Trifonov, E. N., Sussman,J. L. The pitch of chromatin DNA is reflected in its nucleotide sequence. (1980) Proc Natl Acad Sci USA 77(7): 3816- 3820.
- 22. Herzel,H., Weiss, O.,Trifonov, E.N. 10-11 bpperiodicities in complete genomes reflect protein structure and DNA folding.(1999) Bioinformatics 15(3): 187- 193.
- 23. Wentian Li. The study of correlation structures of DNA sequences: a critical review. (1997) Comput Chem 21(4): 257- 271.
- 24. Nair, A. S. S.,Mahalakshmi, T. Visualization of genomic data using inter-nucleotide distance signals.(2005) Proceedings of IEEE Genomic Signal Processing: 408.
- 25. Afreixo, V., Carlos,A.C.B., Armando,J. P.,et al. Genome analysiswithinter-nucleotide distances. (2009) Bioinformatics 25(23): 3064- 3070.
- 26. Hackenberg, M., Rueda, A.,Carpena, P., et al.Clustering of DNA words and biological function: A proof of principle. (2012) J Theor Biol 297: 127- 136.
- 27. Bastos,C.A., Afreixo,V., Pinho,A.J., et al. Inter-dinucleotide distances in the human genome: an analysis of the whole-genome and protein-codingdistributions. (2011) J Integr Bioinform 8(3): 172.
- 28. Bastos,C.A., Afreixo,V., Pinho,A.J., et al.Distances between dinucleotides in the human genome. In 5th International Conference on Practical Applications of Computational Biology & Bioinformatics (PACBB 2011). (2011) Springer 93: 205- 211.
- 29. Fofanov, Y.,Luo, Y., Katili,C. How independent are the appearances of n-mers in different genomes? (2004) Bioinformatics 20(15): 2421- 2428.
- 30. Gabriele, F., Filippo, M., Antonio, R., et al. Word assembly through minimal forbiddenwords. (2006) Theoretical Computer Science 359(1): 214- 230.
- 31. Hampikian, G., Andersen, T. Absent sequences: nullomers and primes. (2007)Pac Symp Biocomput: 355- 366.
- 32. Chor, B., Horn,D., Goldman,N., et al. Genomic DNA k-mer spectra: models and modalities. (2009) Genome Biol 10(10): R108.
- 33. Mehlhorn, K., Näher, S. Leda: A platform for combinatorial and geometric computing. (1995) Communications of the ACM 38(1): 96- 102.
- 34. Christopher, D. M., Mihai, S., John, B. et al. The Stanford CoreNLPnatural language processing toolkit. (2014) In Proceedings of 52nd Annual Meeting of the Association for Computational Linguistics: System Demonstrations 55- 60.
- 35. Doring,A., Weese,D., Rausch,T., et al. SeqAn an efficient, generic C++ library for sequence analysis. (2008) BMC bioinformatics 9(1): 11.
- 36. Stajich,J. E., Block, D., Boulez, K., et al. The Bioperl toolkit: Perl modules for the life sciences. (2002) Genome Res 12(10): 1611- 1618.
- 37. Holland, R.C., Down, T.A., Pocock, M., et al. BioJava: an open-source framework for bioinformatics. (2008) Bioinformatics 24(18): 2096- 2097.
- 38. Gentleman, R. C., Carey, V. J., Bates, D.M., et al. Bioconductor: open software development for computational biology and bioinformatics. (2004) Genome Biol 5(10): R80.
- 39. Smyth,W.F., Yusufu, M. Computing regularities in strings. InComputer Science and Information Technology (2009). ICCSIT. 2nd IEEE International Conference 298- 302.
- 40. Abouelhoda, M. I., Kurtz, S., Ohlebusch, E. Replacing suffix trees with enhanced suffix arrays. (2004) Journal of Discrete Algorithms 2(1): 53- 86.
- 41. Kurtz,S., Narechania, A., Stein, J.C., et al. A new method to compute K-mer frequencies and its application to annotate large repetitive plant genomes. (2008) BMC genomics 9(1): 517.
- 42. Manber,U., Myers, G. Suffix arrays: a new method for on-line string searches. (1993) SIAM J. Comput 22(5): 935- 948.
- 43. Kullback,S., Leibler, R. A. On information and sufficiency. (1951) The Annals of Mathematical Statistics 22(1): 79- 86.
- 44. Smirnov, N.V. On the estimation of the discrepancy between empirical curves of distribution for two independent samples. (1939) Bull. Math. Univ. Moscow 2: 3- 14
- 45. Carpena, P., Bernaola-Galvan, P., Hackenberg, M., et al. Level statistics of words: Finding keywords in literary texts and symbolic sequences. (2009) Phys Rev E 79(3): 035- 102.