Methodology for Evaluating The Properties of Carbon Nano Tubes for Engineering Applications
B. S. Sindu1,2*, Saptarshi Sasmal1,2 and Smitha Gopinath1,2
Affiliation
- 1Academy of Scientific and Innovative Research, CSIR Campus, Taramani, Chennai-600113, INDIA
- 2CSIR-Structural Engineering Research Centre, CSIR Campus, Taramani, Chennai-600113, INDIA
Corresponding Author
Sindu BS, Academy of Scientific and Innovative Research, CSIR Campus, Taramani, Chennai-600113, INDIA, E-mail: sindu@serc.res.in; sindu.lsn@gmail.com
Citation
B. S. Sindu., et al. Unified Approach to evaluate properties of Carbon Nano Tubes for Engineering Applications. (2014) J Nanotech Mater Sci 1(1): 1- 6.
Copy rights
© 2014 Sindu, B.S. This is an Open access article distributed under the terms of Creative Commons Attribution 4.0 International License.
Keywords
Carbon nanotube; Elastic modulus; Nanoscale continuum theory; Finite element analysis
Abstract
Owing to the superior mechanical properties of Carbon Nanotubes (CNTs), research has been initiated to use this nanomaterial in construction industry. The elastic modulus of CNT is of great importance in order to use CNTs in construction industry.for judicious and effective application of CNT in construction industry where mass scale utilization is inhabitable,it is important to accurately assess the properties of CNTs since these nano fiber materials are extremely cost sensitive. There is no well established tool or method available for the engineers to determine the properties of CNT, other than to accept the manufactures data. Nanoscale continuum theory uses a representative volume to determine the elastic modulus which not include the effect of radius and aspect ratio. In the present study, numerical model is developed and the validated one is used to study the effects of geometrical variabilities on the properties of CNT. Further, a unified approach is proposed to determine the mechanical properties, such as tensile stiffness, of the Carbon nanotube with a given structural arrangement (chirality and radius)if the same for the basic configuration, graphene, is known. The procedure discussed and the unified approach proposed in the present study will be helpful to the engineers to easily estimate the properties such as elastic modulus or tensile stiffness of CNTs before application with conventional materials for developing new materials with enhanced properties.
Introduction
Carbon nanotube (CNT) is a cylindrical nanostructure which could be thought of formed by rolling of a graphene sheet. The radius of the nanotube ranges from 0.3nm - 100nm and has a very high aspect ratio. CNT may be single walled or multi-walled. Single Walled Nanotube (SWNT) is a single sheet graphene rolled into a cylinder and Multi Walled Nanotube (MWNT) has many layers of graphene sheet rolled coaxially around a hollow core. Iijima[1] discovered the CNT while studying the carbon produced by arc evaporation of graphite in the helium atmosphere using High Resolution Transmission Electron Microscopy (HRTEM). Since then, various experimental and theoretical studies have been carried out by researchers around the world to determine its mechanical, chemical and electrical properties.
Ruoff and Lorrents[2] reported that CNTs possess superior mechanical properties and can be used as a potential reinforcing material to develop composites of desirable mechanical properties. Konsta-Gdoutos et al.[3] found that the macro and nano-properties of cement increased by dispersion of MWNT using ultrasonic energy and use of surfactant. Experiments conducted by Tyson et al.[4] on cement reinforced by 0.1 and 0.2 weight percentage of CNTs showed that the flexural strength, ductility, strain to failure, elastic modulus and fracture toughness of the material also increased.
The elastic modulus of CNT is of great importance for developing a composite material by adding CNTs. Various researchers carried out experimental studies based on techniques using HRTEM, Scanning Electron Microscopy (SEM) and Atomic Force Microscopy (AFM) to determine the elastic modulus of SWNTs and MWNTs. The elastic modulus of CNT reported by each researcher is scattered and found to fall in a range of 1TPa to 6TPa. Treacy et al.[5] observed the thermal vibrations of MWNT in TEM and reported its elastic modulus to be in the range of 0.4 - 4.15TPa with an average of 1.8TPa. Characteristics of SWNT in room temperature were observed by Krishnan et al.[6] using Transmission Electron Microscopy and its elastics modulus was found to vary in the range of 0.9 - 1.7TPa with an average of 1.25TPa. The elastic modulus of an individual MWNT was reported as 1TPa based on its cross sectional analysis in SFM (Scanning Force Microscopy)[7]. The cooling-induced compressive deformation of CNT was monitored by micro-Raman Spectroscopy by Lourie and Wagner[8] and the elastic modulus of SWNT and MWNT was derived to be in the range of 2.8−3.6 TPa and 1.7−2.4 TPa respectively. Tensile tests were conducted by pulling MWNT using AFM tips and its behaviour was observed under Scanning Electron Microscope (SEM). The tensile strength and the stiffness of MWNT obtained by this method was 11−63 GPa and 0.27− 0.95[9].
Many theoretical studies using molecular dynamics, tight binding methods and continuum studies were also carried out to determine the elastic modulus of CNT and it was found that there was a large variations in elastic modulus of CNT. Molecular dynamics simulation was carried out using[11,12] interatomic potential and the response of SWNT subjected to compression was studied. An empirical relationship was given by Cornwell and Wille[12] to determine the elastic modulus of the CNT with respect to its radius. Prylutskyy et al.[13]carried out molecular dynamics studies using potentials based on bond stretching and bond angle changes and determined the elastic modulus as 1.1 −1.2TPa. Analytical expressions were obtained by Popov and Van Doren[14] to determine the elastic modulus of different chiral nanotubes using Borns perbutation technique for a lattice - dynamical model. The elastic modulus of nanotube was reported in Vaccarini et al.[15], as 1.26TPa using non-orthogonal tight binding method.
In continuum mechanics studies carried out by Yakobson et al.[16], CNTs were modeled as a thin shell, a beam or many truss members. The continuum shell model was used to study the behavior of CNT beyond the elastic limit. CNT was modeled as a beam and its elastic modulus was determined by measuring the resonant frequency and using modulus frequency relationship[17]. Odegard et al.[18] used truss members to determine the effective bending rigidity of CNT using equivalent continuum method. Nanoscale continuum theories have been established which links the continuum models with atomic simulations. Quasi-continuum method was developed in which atomistic simulations were carried out near the deformations and continuum analysis was carried out far away from the deformations thereby reducing the redundant degrees of freedom[19]. A nanoscale continuum theory of fracture nucleation in SWNT was developed incorporating the interatomic potentials[20].
The nanoscale continuum theory was applied by Zhang et al.[21] to study the linear elastic modulus of SWNT using multi-body interatomic potential and considering the non-centrosymmetric structure of CNT. It was observed that the elastic modulus of CNT determined by each method is found to vary and it lies in a range from 1TPa to 6TPa. It is difficult to conduct experiments at nanoscale and to establish atomistic studies because of the huge computational efforts and sophisticated instrumentations. Hence, a simplified mathematical model is developed to determine elastic modulus of CNT of armchair and zigzag tubes using nanoscale continuum theory developed by Zhang et al.[21] and a numerical model developed by Jalalahmadi and Naghdabadi[22].
Though few researchers[23-25] have taken into account the geometry of CNT for analytical and atomisticcomputation of its mechanical properties, studies on the influence of geometric parameters, both local (such as chirality) and global (such as aspect ratio), of CNTs have not been paid considerable attention. However, for engineering applications, it is important to evaluate the properties of CNTs with different geometrical configurations for judicious and appropriate application in enhancing/engineering various types of composites. The representative volume taken to determine the elastic modulusdoes not take into account effect of the geometry of the nanotube and its chirality. Hence, the tensile stiffness and so the elastic modulus of any type of CNT obtained by this method will be the same which is found to be incorrect and highly conservative as the advantage due to the curvature of the tubes will not reflect in the mechanical properties. But, in order to take the advantage of higher modulus of CNT compared to graphene for civil engineering applications the effect of curved structure and its chirality should be taken into account. Hence, a validated finite element model has been used to study the effect of various parameters like chirality, tube radius and aspect ratio on the elastic modulus of CNT. A methodology using interatomic potential is proposed for determining the tensile stiffness of CNTs with different geometrical arrangements.
Geometry of Carbon nanotubes
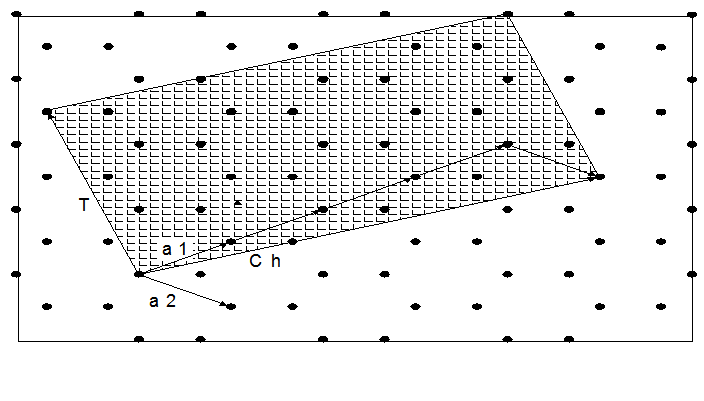
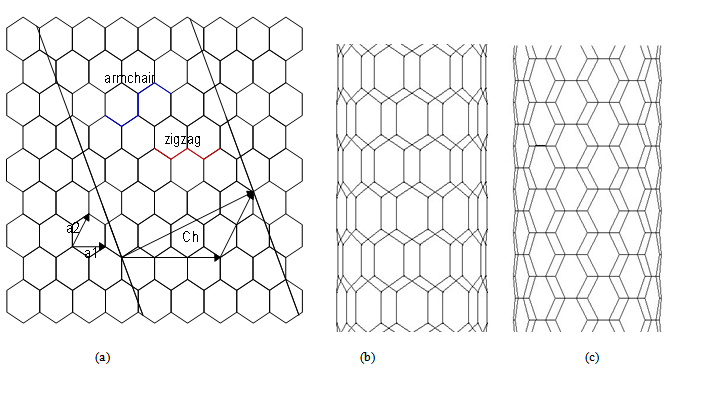
Carbon nanotubes can be specified by two different parameters, viz., its length and chirality. Chirality of a carbon nanotube is specified by the multipliers of two base vectors in a chiral vector. A chiral vector is the one along which the graphene sheet can be rolled to form a carbon nanotube. A graphene sheet can be assumed to have two base vectors along two directions of its crystal lattice, (→a1) and (→a2) as shown in Figure. 1.
The chiral vector (Ch)→ can be obtained by the summation of these two base vectors. Thus, the chiral vector is given by equation
(Ch)→ = m(→a1) + n(→a2) (1)
where m and n are the multipliers of the base vectors (→a1) and (→a2) respectively.In this case, the chirality of this nanotube is denoted as (m,n). There is another vector called translational vector T→ which is perpendicular to chiral vector along the length of the nanotube defined as
T→ = t1(→a1) + t2(→a2) (2)
where t1 = (2n + m)/dR and t2 = (2m + n)/dR in which
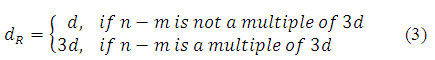
And d is the highest common divisor of (n,m).
A rectangle bounded by vectors (Ch)→ and T→ forms a unit cell of a carbon nanotube. There are two common types of nanotubes based on the way the graphene sheet is rolled to form CNT; they are zigzag and armchair (Figure. 2). If the chirality of nanotube is (n,0),it is called zigzag nanotube and if it is (n,n), it is called armchair nanotube.
Since the chiral vector is rolled to form a tube, the length of the chiral vector is equal to the circumference of the nanotube. The length of the chiral vector is given by:
L = √3l 0√(n2 + m2 +nm) (4)
Where l0 is the carbon-carbon bond length in the graphene sheet which is 1.421Å.
Hence, the diameter of the nanotube is given by
d = √3l 0√(n2 + m2 +nm)/π (5))
Interatomic potential and Nanoscale continuum theory
Interatomic potential of a bond denotes the potential energy stored in it under deformation. In order to properly capture the interatomic interactions of the carbon nanotube, it is insufficient to have an interatomic potential that accounts only the effect of change in the desired carbon-carbon bond length.The bond angle and the position of carbon atoms near the desired carbon-carbon bond should also be taken into account. Among many empirical interatomic potentials proposed for carbon-carbon bonds, the most widely accepted one is the Tresoff-Brenner[10,11] potential which takes into account these multi-body effects also.The interatomic potential for a bond between two carbon atoms i and j was developed by Tersoff[10] and Brenner[11] and is given as
Vij = VR(r)ij - BijVA(r)ij (6)
where rij is the distance between atoms i and j. VR(r)ij and VA(r)ij are repulsive and attractive pair potential terms which represent repulsive and attractive forces between atoms i and j.
A nanoscale continuum theory was proposed in Zhang et al. (2002b) by which the macroscopic deformation of the material can be linked with the interatomic potential and the atomic structure of the material. This is achieved through Cauchy-Born rule of crystal elasticity, by equating the strain energy of the material at the continuum level to potential energy stored in the bonds due to the imposed deformation. This is given by
W = (1/2Ωe)Σi,jV(ri,j) (7)
where W is the strain energy density of the representative cell and V(ri,j)is the interatomic potential of the atomic bond between atoms i and j which denotes the potential energy stored in it when it is subjected to deformation. Ωe is the volume of the representative cell which is equal to (3√ 3 /4)(l 0)2.
where, l 0 is the unstretched bond length of a carbon-carbon atom in carbon nanotube. The factor 1/2 comes due to the equal splitting of bond energy to each atom.
From nanoscale continuum theory, linear elastic modulus tensor can be obtained using
C = [∂2W/∂EG∂EG - ∂2W/∂EG∂x .∂2W/∂x∂x) -1.∂2W/∂x∂EG]EG=0, x = 0 (8)
Let Z denote the axial direction of SWNT and θ denote the circumferential direction of SWNT. The non-vanishing terms of the linear elastic modulus tensor are CZZZZ, Cθθθθ and CZZθθ=CθθZZ. Hence, for a simple tension along the axial direction of SWNT, the elastic modulus is given by
Einter= CZZZZ - C2θθθθ/Cθθθθ (9)
The elastic modulus tensor and the linear elastic modulus obtained are actually the tensile stiffness, i.e., modulus multiplied by thickness rather than the modulus. By using Eqn. (9), linear elastic tensile stiffness of CNT with interatomic potential given by Brenner[11] is obtained as 159N/m. This value was proposed as the tensile stiffness of CNTs when the effect of curvature is not taken into account. In the present study, the same is used to normalize the results obtained for tensile stiffness of CNTs by considering the effect of curvature (discussed in section 5).
Numerical Simulation
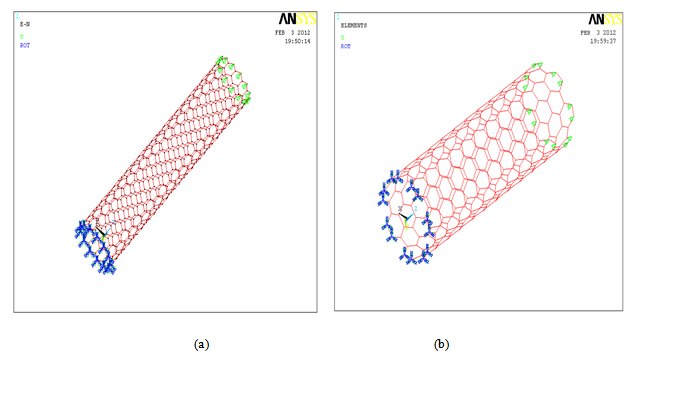
The linear elastic tensile stiffness as obtained above does not depend upon the chirality of the nanotube and the tube radius. In order to find out the dependence of elastic modulus of SWNT on parameters like chirality, tube radius and the aspect ratio, a study has been carried out on the numerical simulation of carbon nanotube. A 3-D Finite Element Model was created in ANSYS in which nodes were placed in the location of carbon atoms and the covalent bonds between the carbon atoms were replaced by three dimensional BEAM 4 elements. BEAM4 element has six degrees of freedom and is defined by two nodes as well as its cross-sectional area, two moments of inertia, two dimensions and material properties.
Figure 3: a) Finite Element model of a) (10,0) and b) (7,7) CNT
From classical mechanics, the stretching stiffness, KF and the bending stiffness, KM of the beam are as follows:
KF = EA/L and KM= EI/L (10)
Jalalahmadi and Naghdabadi[22] used Morse potential in which the parameters were changed to fit the Brenner potential and obtained the effective stretching and bending stiffness of the bond as 854nN/nm and 0.9nN.nm/rad2 respectively. Using these values and assuming circular cross-section, the diameter of the beam element is found to be 0.1296 nm and the material used as beam element is found to have the elastic modulus as 9.382TPa. Since the model is in linear regime, the strain energy, U of the SWNT is given by U = 1/2σεAL = 1/2Eε2AL (11)
Where σ is the stress, ε is the strain, E is the elastic modulus, L is the length of the nanotube and A is the area which is equal to πDt in which D is the diameter and t is the thickness of the tube. From this, the elastic modulus of the nanotube can be obtained as E = 2U/ALε2 (12)
A Finite Element model of SWNT of particular diameter and length with the properties as described above is generated in ANSYS software. It is fixed at one end and stretched at the other end thereby producing tensile strain. The total strain energy, U of the SWNT is calculated by summing up the strain energies of each beam element of the generated model and the elastic modulus is calculated using the above expression. It can be found from Table 1 that the elastic modulus of the SWNT obtained from the present study using the Finite Element Modelling agrees well with the results reported in Jalalahmadi and Naghdabadi[22].
Table 1: Validation of the Elastic modulus of CNT obtained from the present study
| Chirality | Elastic modulus (TPa) | |
|---|---|---|
| Present study | Reported in literature [Jalalahmadi and Naghdabadi (2007)] | |
| (7,7) | 3.34 | 3.296 |
| (12,0) | 3.312 | 3.312 |
| (5,9) | 3.392 | 3.514 |
From Table 1, it can be observed that the values obtained in the present work are in good agreement (within 5% deviation) with that reported in the literature. Since the thickness of SWNT is of an atom thick, it is more meaningful to determine the tensile stiffness rather than the elastic modulus of the nanotube. Tensile stiffness of the CNT is obtained by dividing the elastic modulus of the tube by the thickness of the tube.
Study on various parameters
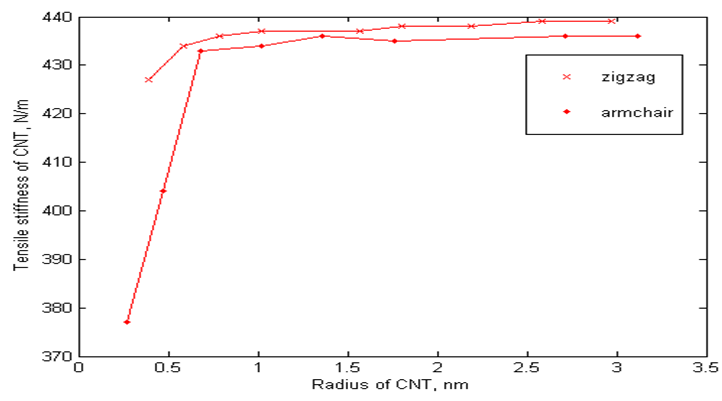
The validated Finite Element Model is used to study the effects of nanotube radius, aspect ratio and chirality of SWNT on its tensile stiffness. The effect of change in radius of the nanotube on the tensile stiffness for two different chiral tubes, viz., zigzag (n, 0) and armchair (n, n) was studied. The radius of the nanotube was varied from 0.3nm to 3nm keeping the aspect ratio constant equal to 6 in both the cases. The tensile stiffness of the nanotube was plotted with respect to the tube radius for two different chiral tubes which is shown in Figure 4.
Figure 4: Tensile stiffness vs radius of CNT for armchair and zigzag
It is seen from the plot that the tensile stiffness of zigzag nanotube was 13% greater than armchair when the radius of the tube was 0.3nm. The difference in tensile stiffness of both the tubes decreased gradually upto the radius of 0.8nm. For nanotubes of radius greater than 0.8nm, the difference in percentage of tensile stiffness of CNT reduced to 0.7%, i.e, almost remained equal. This shows that the tensile stiffness of nanotubes of radius greater than 0.8nm is independent of tube radius and its chirality.
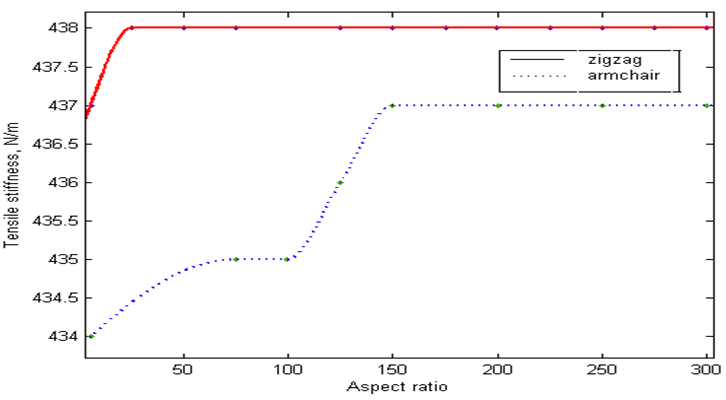
The effect of change in aspect ratio of the nanotube on the tensile stiffness for both the chiral tubes was also studied using the validated Finite Element Model. The aspect ratio of both the chiral tubes was varied from 6 to 300 keeping the radius of the tube constant equal to 1nm in both the cases. The tensile stiffness of the nanotube was plotted with respect to its aspect ratio for both the cases as shown in Figure 5. From the plot, it can be seen that the tensile stiffness of the nanotube varies only by a maximum of 0.9% with respect to its aspect ratio. Hence it is evident that the tensile stiffness is independent of aspect ratio of the tube.
Figure 5: Tensile stiffness of CNT vs aspect ratio for armchair and zigzag CNTs
Determination of the Tensile Stiffness of Carbon Nanotube
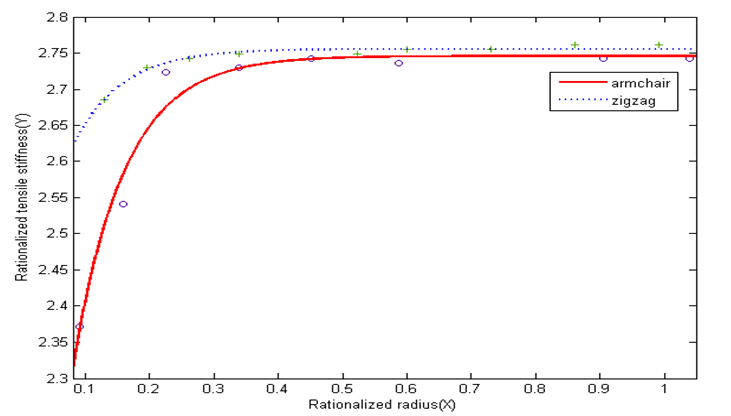
From the above studies, it has been found out that the tensile stiffness of nanotube varies with respect to the radius of the tube, its chirality and is independent of the aspect ratio of the tube. Hence, a methodology to obtain the tensile stiffness of the nanotube of a particular chirality and tube radius which also involves the interatomic interactions has been worked out.To maintain the dimensionality, the tensile stiffness is normalizedas the ratio of the obtained tensile stiffness to the tensile stiffness which accounts only the interatomic interactions and the radius is normalized with respect to the maximum radius taken for the study. A curve is fitted between the normalized tensile stiffness and the normalized radius and shown in Figure 6.
Figure 6: Normalized tensile stiffness and normalized radius
This plot is curve fitted and an expression is obtained. The R² valve of the fitted curve is 0.9719 and 0.9688 for zigzag and armchair respectively. According to the above approach, an expression to determine the tensile stiffness of the Carbon nanotube of a particular chiarlity and radius has been proposed which is as follows:
E = f(Einter, r, chirality) (13)
It is to underscore that the study is carried out with limited number of cases and few key variables. For developing the unified solution or proposing a closed form relation among the variables with the tensile stiffness of CNTs, a large space of samples needs to be investigated and analyzed. The scope of this work is limited to evaluation of mechanical properties of defect free CNTs whereas market available and fabricated CNTs are bound to have defects. With different types of defects, further studies are to be carried out for more generalized results. However, in the current work authors have limited their observations only to the defectfree ones in order to understand the influence of geometrical parameters on the mechanical characteristics of CNTs in detail which would otherwise bring confusion why a particular phenomenon has been observed if the defects were also considered. The present study has been limited to CNTs of two different chiralities, viz., armchair and zigzag. It is found that the local geometrical arrangement play a role on the mechanical behavior of the CNTs. Extrapolation of these observations to CNTs with other chiralities would be over simplification and could be erroneous as well. Therefore, it is to mention that the study on mechanical behavior of other chiral tubes needs further study.
Conclusion
The present study presents a unified approach for determining the tensile stiffness of CNTs. With the known properties of graphene, it is attempted to provide the information on the mechcnical properties of CNTs with different geometries by bridging the knowledge on interatomic potentials with FEM. From the study, it is found that:
i. The tensile stiffness obtained is approximately three times higher than the tensile stiffness obtained by considering the flat configuration. This increase is attributed to the curvature of graphene to form a CNT.
ii. The elastic modulus of the nanotube depends on the chirality of the tube. The elastic modulus of the zigzag nanotube is higher than that of armchair nanotube of same radius.
iii. The elastic modulus of both the chiral tubes of particular radius is independent on the aspect ratio of the tube.
iv. The elastic modulii of both the chiral tubes depend on the radius of the tube upto 0.8nm and remains constant after that.
A methodologyhas been proposed by using the interatomic potential to determine the tensile stiffness of the nanotube where the chirality and radius of the nanotube are the also the parameters. The methodologyproposed in the present study will be helpful to the engineers to easily estimate the properties of CNTs for developing new CNT based improved materials. Further studies are being carried out to determine the mechanical properties of CNT modified cementitious composites where the observations presented here will be extremely useful.
Acknowledgment
This paper has been published under the kind permission of the Director, CSIR-SERC.
References
- 1. Iijima, S. Helical microtubules of graphitic carbon. (1991) Nature 354: 56-58.
- 2. Ruoff, R.S., Lorrents, D.C. Mechanical and thermal properties of carbon nanotubes. (1995) Carbon 33(7): 925-930.
- 3. Konsta - Gdoutos, M.S., Metaxa, Z.S., Shah, S.P. Highly dispersed Carbon nanotube reinforced cement based materials. (2010) Cement and Concrete Research 40(7): 1052-1059.
- 4. Tyson B.M., Abu Al-Rub, R.K., Yazdanbakhsh, A. et al. Carbon nanotubes and carbon nanofibers for enhancing the mechanical properties of nanocomposite cementitious materials. (2011) J Mater Civ Eng 23(7):1028-1035.
- 5. Treacy, M.M.J., Ebbesen, T.W., Gibson, J.M. Exceptionally high Young’s modulus observed for individual carbon nanotubes. (1996) Nature 381: 678-680.
- 6. Krishnan, A., Dujardin, E., Ebbesen, T.W., et al. Young’s modulus of single-walled nanotubes. (1998) Physics Review B. 58(20):14013-14019.
- 7. Muster, J.B., Burghard, M., Roth, S., et al. A Scanning force microscopy characterization of individual carbon nanotubes on electrode arrays. (1998) J Vac Sci Technol B 16: 2796-2802.
- 8. Lourie, O., Wagner, H.D. Evaluation of Young’s modulus of carbon nanotubes by micro - Raman spectroscopy. (1998) J Materials Research 13(9): 2418-2422.
- 9. Yu, M.F., Lourie, O., Dyer, M.J., et al. Strength and breaking mechanism of multiwalled carbon nanotubes under tensile loading. (2000) Science 287(5453): 637-640.
- 10. Tersoff, J. New empirical approach for the structure and energy and covalent systems. (1988) Physical Review B 37(12): 6991-7000.
- 11. Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. (1990) Physical Review B 42(15): 9458-9471.
- 12. Cornwell, C.F., Wille, L.T. Elastic properties of Single-walled Carbon Nanotubes in compression. (1997) Solid State Communications 101(8): 555-558.
- 13. Prylutskyy, Y.I., Durov, S.S. Ogloblya, O.V., et al. Molecular dynamics simulation of mechanical, vibrational and electronic properties of carbon nanotubes. (2000) Computational Materials Science 17(2-4): 352-355.
- 14. Popov, V.N., Van Doren, V.E., Balkanski, M. Elastic properties of single - walled carbon nanotubes. (2000) Physical Review B. 61: 3078-3084.
- 15. Vaccarini, L., Goze, C., Henrard. L., et al. A Mechanical and electronic properties of carbon and boron - nitride nanotubes. (2000) Carbon 38: 1681-1690.
- 16. Yakobson, B.I., Brabec, C.J., Bernholc, J. Nanomechanics of carbon tubes: Instabilities beyond linear response. (1996) Physical Review Letters 76(14): 2511-2514.
- 17. Liu, J.Z., Zheng, Q., Jiang, Q. Effect of a rippling mode on resonances of Carbon Nanotubes. (2001) Physical Review Letters 86(21): 4843-4846.
- 18. Odegard, G.M., Gates, T.S., Nicholson, L.M., et al. Equivalent-continuum modeling of nano-structured materials. (2002) Composites Science and Technology 62(14): 1869-1880
- 19. Shenoy, V.B., Miller, R., Tadmor, E.B., et al. An adaptive finite element approach to atomic-scale mechanics - The quasi-continuum method. (1999) J Physics and Solids 47(3): 611-642.
- 20. Zhang, P., Huang, Y., Gao, H., et al. Fracture nucleation in single-wall carbon nanotubes under tension: a continuum analysis incorporating interatomic potentials. (2002a) J Applied Mechanics 69(4): 454-458.
- 21. Zhang, P., Huang, Y., Geubelle, P.H., et al. The elastic modulus of single-wall carbon nanotubes: a continuum analysis incorporating interatomic potentials. (2002b) International Journal of Solids and Structures. 39(13-14): 3893-3906.
- 22. Jalalahmadi, B., Naghdabadi, R. Finite Element Modeling of single - walled carbon nanotubes with introducing a new wall thickness. (2007) Journal of Physics: Conference Series 61: 497-502.
- 23. Jin, Y., Yuan, F.G. Simulation of elastic properties of single-walled carbon nanotubes. (2003) Composites Science and Technology 63: 1507-1515.
- 24. Liew, K.M., He, X.Q., Wong, C.H. On the study of elastic and plastic properties of multi-walled carbon nanotubes under axial tension using molecular dynamics simulation. (2004) Acta Materialia 52(9): 2521-2527.
- 25. Xiao, J.R., Gama, B.A., Gillespie, J.W. An analytical molecular structural mechanics model for the mechanical properties of carbon nanotubes. (2005) International Journal of Solids and Structures 42(11-12): 3075-3092.