Some Regularities Involved with Oxidation Numbers Stated in Formulation of Redox Systems According to GATES/GEB Principles
Anna Maria Michalowska-Kaczmarczyk1, Aneta Sporna-Kucab2, Tadeusz Michalowski2*
Affiliation
- 1Department of Oncology, the University Hospital in Cracow, 31-501 Cracow, Poland
- 2Department of Analytical Chemistry, Technical University of Cracow, 31-155 Cracow, Poland
Corresponding Author
Tadeusz Michalowski, Department of Analytical Chemistry, Technical University of Cracow, 31-155 Cracow, Poland, michalot@o2.pl
Citation
Tadeusz Michalowski, T., et al. Some Regularities Involved with Oxidation Numbers Stated In Formulation of Redox Systems According to GATES/GEB Principles. (2017) J Anal Bioanal Sep Tech 2(2): 102- 110.
Copy rights
© 2017 Michalowski, T. This is an Open access article distributed under the terms of Creative Commons Attribution 4.0 International License.
Keywords
Electrolytic systems; Redox systems; GEB; GATES; Oxidation number
Abstract
Formulation of Generalized Electron Balance (GEB) for redox systems according to Approach II to GEB does not require the prior knowledge of oxidation numbers of all elements in components forming a system, and in the species of the system thus formed. This formulation is involved with linear combination of charge and elemental and/or core balances related to the system in question. The skillful choice of multipliers for the balances on the step of purposeful formulation of this linear combination allows for to find important regularities for electrolytic systems of different degree of complexity. These multipliers are related to the oxidation numbers of the elements; this regularity is important in the context of the fact that the oxidation number is the contractual concept. This property is valid for redox and non-redox systems. In this context, oxidation number is perceived as the derivative/redundant concept. The paper indicates the close relationships between different rules of conservation and indicates huge possibilities inherent in the generalized approach to electrolytic systems (GATES), and GATES/GEB in particular.
Introduction
The paper refers critically to some fundamental concepts, known to a wide community of chemists from early stages of education. It concerns the terms: oxidation state/number; oxidant and reductant; equivalent weight. All those concepts, defended by IUPAC, raise many reservations and controversies, expressed in our review papers issued in recent years[1-5], and discussed elsewhere[6-8]. All these terms were introduced/considered in context of stoichiometry, i.e., the concept straight from the 18th century[3]. The factual place of these terms is indicated here by the mathematical formulation of redox systems, realized according to GATES/GEB principles, i.e., based on the Generalized Approach to Electrolytic Systems (GATES)[9], with Generalized Electron Balance (GEB) formulated according to Approach II to GEB[1-5,9-15].
Within GATES/GEB, the species in electrolytic systems are considered in their natural form, particularly as hydrates Xizi.niw in aqueous solutions[10], where zi(zi = 0, ± 1, ± 2,…) is the charge of Xizi, expressed in elementary charge unit e = F/NA (F – Faraday constant, NA – Avogadro’s constant), and niW ( ≥ 0) is the mean number of water (W = H2O) molecules attached to Xizi. The known chemical formulas of the Xizi of the and their respective external charges provide the information necessary/sufficient to formulate the respective balances[4].
The terms: components and species are distinguished. In the notation applied here, N0j (j = 1,2,…,J) is the number of molecules of components of j-th kind composing the static or dynamic D+T system, whereby the D and T are composed separately, from defined components, including water. The mono- or two-phase electrolytic system thus obtained involve N1 molecules of H2O and Ni species of i-th kind, Xiziniw (i = 2, 3,…,I), denoted briefly as Xizi (Ni, ni), where ni ≡ niz ≡ niH2O; then we have: H+1 (N2,n2), OH-1 (N3,n3),… .
The GEB is formulated according to two equivalent approaches, named as the Approach I to GEB and the Approach II to GEB. The Approach I to GEB is formulated according to ‘card game’ principle[10]; it is based on a common pool of electrons introduced into the system by electron-active elements[10-15]. The Approach II to GEB is formulated from linear combination 2.f(O) – f(H) of elemental balances: f(H) for H, and f(O). Both Approaches (I and II) to GEB are equivalent.
∴ Approach II to GEB <=> Approach I to GEB (1)
All the inferences made within GATES/GEB are based on firm, algebraic foundations. The approach proposed allows understanding far better all physicochemical phenomena occurring in the system in question and improving some methods of analysis. All the facts testify very well about the potency of simulated calculations made, according to GATES, on the basis of all attainable physicochemical knowledge.
The Approach I to GEB needs prior knowledge of oxidation numbers. The Approach II to GEB does not require any prior knowledge of the oxidation numbers of elements in the components and in the species. Because the ‘oxidation number’ is essentially the contractual concept, it is a fact of capital importance, particularly in relation to organic species (molecules, ions, radicals and ion-radicals) of any degree of complexity. However, when the oxidation numbers are easily determined, the Approach I to GEB, known as the ‘short’ version of GEB, can be applied. The roles of oxidants and reductants are not assigned a priori to individual components within the Approaches I and II to GEB; GATES/GEB provides full ‘democracy’ in this regard.
The principle of GEB formulation, discovered by Michalowski (1992) as the Approach I to GEB, and 2006 as the Approach II to GEB) was unknown in earlier literature. The GEB is considered as a new law of the matter conservation related to electrolytic redox systems, as a Law of Nature[9,10].
The importance of GATES/GEB in area of electrolytic redox systems is unquestionable. Then the main purpose of the present paper is to familiarize it to a wider community. It will also be indicated, in a simple mathematical manner, the fundamental criterion distinguishing between non-redox and redox systems. Contrary to appearances, this criterion is not immediately associated with free electrons in electrolytic system.
In this paper we consider first a relatively simple dynamic redox system, where V mL of C mol/L NaOH as titrant T is added; up to a given point of the titration, into V0 mL of C0 mol/L Br2 as titrant D and the D+T mixture with volume V0+V is thus obtained.
V0 mL of D is composed of Br2 (N01 molecules)+H2O (N02 molecules), and V mL of T is composed of NaOH (N03 molecules)+H2O (N04 molecules). In V0+V mL of D+T mixture we have the following species:
H2O (N1), H+1 (N2,n2), OH-1 (N3,n3), HBrO3 (N4,n4), BrO3-1 (N5,n5), HBrO (N6,n6), BrO-1 (N7,n7), Br2 (N8,n8), Br3-1 (N9,n9), Br-1 (N10,n10), Na+1 (N11,n11). (2)
In the D+T mixture, the molar concentrations of the species are as follows:
[Xiiz] . (V0+V) = 103.Ni/NA (i = 2,…,11) (3)
And molar concentrations of the solutes are equal to
C0.V0 = 103.N01/NA (4)
C.V = 103.N03/NA (5)
At V = 0, from Eq. (3) we have
[Xizi] .V0 = 103.Ni/NA (i = 2,…,11) (6)
The system considered above will be denoted as T => D or, more exactly, as
System-1: NaOH (C, V) => Br2 (C0, V0)
At V = 0, the D+T is limited to D, i.e., C0mol/L Br2 solution. Analogously, we apply the notation
System-2: NaOH (C, V) => HBrO (C0, V0)
for the second system, considered in further parts of this paper. At V = 0, the System 2 is limited to C0 mol/L HBrO solution. The C0 mol/L Br2 and C0 mol/L HBrO are considered as static systems, obtained after disposable mixing of the related components.
Formulation of balances for the System-1
Charge balance
Denoting atomic numbers: ZH for H, Z0 for O, ZBr for Br, ZNa for Na we have the balances:
• For nuclear protons
(2ZH+Z0)N1+(ZH+n2(2ZH+Z0))N2+(ZH+Z0+n3(2ZH+Z0))N3+(ZH+ZBr+3Z0+n4(2ZH+Z0))N4+(ZBr+3Z0+n5(2ZH+Z0))N5+(ZH+ZBr+Z0+n6(2ZH+Z0))N6+(ZBr+Z0+n7(2ZH+Z0))N7+(2ZBr+n8(2ZH+Z0))N8+(3ZBr+n9(2ZH+Z0)) N9+(ZBr+n10(2ZH+Z0))N10+(ZNa+n11(2ZH+Z0))N11 = 2ZBrN01+ (2ZH+Z0)N02+ (ZNa+Z0+ZH)N03+ (2ZH+Z0)N04 (7)
• For orbital electrons
(2ZH+Z0)N1+(ZH-1+n2(2ZH+Z0))N2+(ZH+1+Z0+n3(2ZH+Z0))N3+(ZH+ZBr+3ZO+n4(2ZH+Z0))N4+(ZBr+3Z0+1+n5(2ZH+Z0))N5+(ZH+ZBr+Z0+n6(2ZH+Z0))N6+(ZBr+Z0+1+n7(2ZH+Z0))N7+(2ZBr+n8(2ZH+Z0))N8+(3ZBr+1+n9(2ZH+Z0))N9+(ZBr+1+n10(2ZBr+Z0))N10+(ZNa–1+n11(2ZH+Z0))N11 = 2ZBrN01+(2ZH+Z0)N02 (8)
Subtraction of Equation-(8) from Equation-(7) gives the charge balance (ChB)
f0 = ChB : N2 – N3 – N5 – N7 – N9 – N10+N11 = 0 ↔ (+1)N2+(–1)N3+(–1)N5+(–1)N7+(–1)N9+(–1)N10+(+1)N11 = 0 (9)
The charge balance (f0 = ChB) is then derivable from balances for electrons and protons. It is nothing strange because the external charge of a species is a simple sum of charges brought by nuclear protons and orbital electrons.
In particular, from Equations (3) and (9) we have
[H+1] – [OH-1] – [BrO3-1] – [BrO-1] – [Br3-1] – [Br-1]+[Na+1] = 0 → (9a)
(+1).[H+1]+(–1).[OH-1]+(–1).[BrO3-1]+(–1).[BrO-1]+(–1).[Br3-1]+(–1).[Br-1]+(+1).[Na+1] = 0 (9b)
Generally, ChB is expressed by equation
∑izi . Ni = 0 ↔ ∑izi . [Xizi = 0 10
Note that zi ≠ 0 are multipliers for concentrations of the corresponding ions in the ChB.
Elemental balances
f1 = f(H) : 2N1+N2(1+2n2)+N3(1+2n3)+N4(1+2n4)+2N5n5+N6(1+2n6)+2N7n7+2N8n8+2N9n9+2N10n10 = 2N02 (11)
f2 = f(O) : N1+N2n2+N3(1+n3)+N4(3+n4)+N5(3+n5)+N6(1+n6)+N7(1+n7)+N8n8+N9n9+N10n10 = N02 (12)
f3 = f(Br) : N4+N5+N6+N7+2N8+3N9+N10 = 2N01 (13)
–f4 = –f(Na) : N03 = N11 (14)
Linear combinations of the balances
From Eqs. (11) and (12) we have
f12 = 2.f2 – f1: – N2+N3+5N4+6N5+N6+2N7 = 0 (15)
From Eqs. (15) and (9)
f12+f0 – f4: 5N4+5N5+N6+N7 – N9 – N10 = 0 (16)
From Eqs. (13) and (16)
ZBr.f3 – (f12+ f0 – f4): (ZBr-5)(N4+N5)+(ZBr–1)(N6+N7)+2ZBrN8+(3ZBr+1)N9+(ZBr+1)N10 = 2ZBrN01 (17)
Formulation of balances for the System 2
In the System 2 we have the set (2) of the species identical as in the System 1. Applying similar notation, we assume that V0 mL of D is composed of HBrO (N01 molecules)+H2O (N02 molecules) and V mL of T is composed of NaOH (N03 molecules)+H2O (N04 molecules). The numbers N01 and N02 of the molecules composing these systems and the numbers Ni of the species in the System 2 are different than that in the System 1, in principle. The f0 = ChB in the System 2 is identical with Eq. (9a), and –f4 = –f(Na) is identical with Eq. (14). Then after formulation of f1 and f2 we have here, by turns,
f12 = 2.f2 – f1 :– N2+N3+5N4+6N5+N6+2N7 = N01+N03 (18)
f3 = f (Br) : N4+N5+ N6+N7+2N8+3N9+N10 = N01 (19)
f12+f0– f4 : 5N4+5N5+N6+N7 – N9 – N10 = N01 (20)
ZBr.f3 – (f12+f0–f4): (ZBr–5)(N4+N5)+(ZBr–1)(N6+N7)+2ZBrN8+ (3ZBr+1)N9+(ZBr+1)N10 = (ZBr–1)N01 (21)
The balances in terms of molar concentrations
For the System 1, from Eqs. (3) – (5), (13), (14) and (16), we have:
([HBrO3]+[BrO3-1])+([HBrO]+[BrO-1])+2[Br2]+3[Br3-1]+[Br-1] = 2.C0V0/ (V0+V) (13a)
[Na+1] = CV/(V0+V) (14a)
5([HBrO3]+[BrO3-1])+([HBrO]+[BrO-1]) – [Br3-1] – [Br-1] = 0 (16a)
Eqs. (13a) and (14a) are termed as concentration balances, obtained from elemental balances (13) and (14), and Eq. (16a) is the shortest form of GEB. The relation (14a) can be immediately introduced into Eq. (9a); then we get
[H+1] – [OH-1] – [BrO3-1] – [BrO-1] – [Br3-1] – [Br-1]+CV/ (V0+V) = 0 (9c)
Eqs. (9c), (13a) and (16a) form the complete set of balances related to the System 1.
For the System 2, from Eqs. (3) – (5), (19) and (20), we obtain the balances:
([HBrO3]+[BrO3-1])+([HBrO]+[BrO-1])+2[Br2]+3[Br3-1]+[Br-1] = C0V0/ (V0+V) (19a)
5([HBrO3]+[BrO3-1])+([HBrO]+[BrO-1]) – [Br3-1] – [Br-1] = C0V0/ (V0+V) (20a)
completed by the balance (9c).
We can also refer to static systems, formed by (a) C0 mol/L Br2 and (b) C0 mol/L HBrO. These solutions are identical with the titrand D in the related Systems 1 and 2. The balances for these static systems are obtained assuming V = 0 in Eqs. (9c), (13a) and (14a), or in Eqs. (9c),(19a) and (20a), resp.
Note that Br2 and HBrO do not oxidize water molecules, i.e., products of H2O oxidation do not exist there as species.
Relations between concentrations of the species
From the interrelations obtained on the basis of expressions for equilibrium data[16] collected in Table 1 we have:
[H+1] = 10-pH; [OH-1] = 10pH-14; [BrO3-1] = 106A(E-1.45)-pBr+6pH; [BrO-1] = 102A(E-0.76)-pBr+2pH-28; [Br2] = 102A(E-1.087)-2pBr; [Br3-1] = 102A(E-1.05)-2pBr; [HBrO3] = 100.7-pH.[BrO3-1]; [HBrO] = 108.6-pH.[BrO-1]
Where the uniformly defined scalar variables: E, pH and pBr, forming a vector x = (E, pH, pBr)T, are involved:
A.E = –log[e-1], pH = –log[H+1], pBr = –log[Br-1]
All the variables are in the exponents of the power for 10 in: [e-1] = 10-A.E, [H+1] = 10-pH, [Br-1] = 10-pBr, where 1/A = RT/F.ln10; A = 16.9 at T = 298 K. The number of the (independent) variables equals to the number of equations, 3 = 3; this ensures a unique solution of the equations related to the Systems 1 and 2, at the preset C0, C and V0 values, and the V-value at which the calculations are realized, at defined step of the calculation procedure, according to iterative computer program presented in Appendix.
Graphical presentation
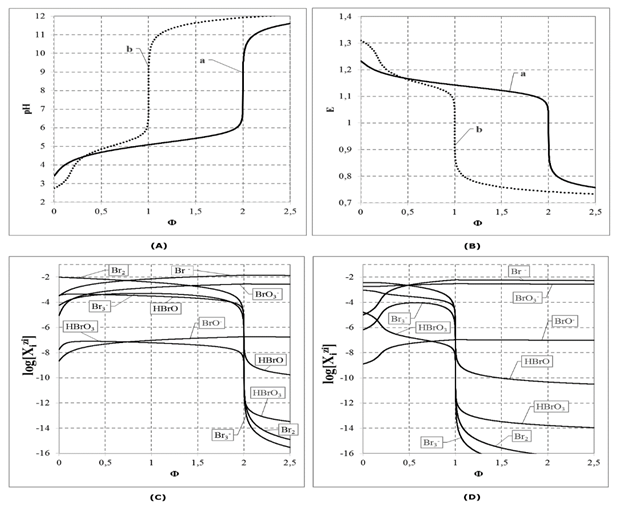
Formulation of the static system with Br2 (C0) was presented first in[17], whereas the dynamic Systems: 1 and 2 were presented in[18]. The pH = pH (Φ) and E = E (Φ) relationships for the Systems 1 and 2 are plotted in Figures 1A, B, where the fraction titrated
C . V
Φ = ---------- (22)
C0. V0
introduces a kind of normalization(independence on V0 value) for the related titration curves. The computer program related to the System 1 is presented in Appendix. Speciation diagrams for the Systems 1 and 2 are presented in Figures 1C, D.
The Br2 solution is acidic, as results e.g. from the ChB (Eq. 9c) at V = 0: at [Na+1] = 0 (Φ = 0) we have: [H+1] – [OH-1] = [BrO3-1]+[BrO-1]+[Br3-1]+[Br-1] > 0, i.e. [H+1] > [OH-1]. The Br2 is an acid with a strength comparable to that of acetic acid; at C0 = 0.01, pH equals: 3.40 for Br2, and 3.325 for CH3COOH (pK1 = 4.65). Disproportionation of Br2occurs initially to a small extent (several %), according to the scheme Br2+OH-1 = HBrO+Br-1.
In the System 2, disproportionation of HBrO affected by NaOH (C) added according to titrimetric mode is presented in Fig. 1D [18]. The [Br-1]/ [BrO3-1] ratio equals: 10-2.2553/10-2.5563 at Φ = 2.0; 10-2.2730/10-2.5740 at Φ = 2.5, i.e. 100.3010 = 2 = 2:1, corresponding to the stoichiometric ratio of products of this reaction. As results from Fig. 1D, the disproportionation of HBrO, at an excess of NaOH added, occurs mainly according to the scheme 3HBrO+3OH-1 = 2Br-1+BrO3-1+3H2O (stoichiometry 3:3 = 1:1), resulting from half-reactions: HBrO+2e-1+H+1 = Br-1+H2O, HBrO – 4e-1+2H2O = BrO3-1+5H+1, and 3H+1+3OH-1 = 3H2O. The (Φ,pH,E) values from the close vicinity of the corresponding equivalence (eq) points on the curves in Figs. 1A,B are collected in Table 2.
In C0 = 0.01 mol/L HBrO, more than 90% HBrO disproportionates according to the reaction 5HBrO = BrO3-1+2Br2+2H2O+H+1; at V = 0 we have: [Br2] = 10-2.4406, [BrO3-1] =
10-2.7442, i.e. [Br2]/ [BrO3-1] = 100.3036 ≈ 2, which confirms this stoichiometry of the reaction. The H+1 ions formed in this reaction acidify the solution significantly: at C0 = 0.01 and V = 0 we have pH = 2.74, although HBrO itself is a relatively weak acid.
Figure-1. The relationships: (A) pH = pH(Φ) and (B) E = E(Φ) for the Systems 1 and 2, and the related speciation diagrams for the Systems: 1 (C) and 2 (D), at V0 = 100, C0 = 0.01, C = 0.1.
The main task of titration is the estimation of the equivalent volume, Veq, corresponding to the volume V ≡ Veq of T, where the fraction titrated (Eq. (22)) assumes the value
C . Veq
Φeq= ------------- (23)
C0. V0
in contradistinction to visual titrations, where the end volume Ve Veq is registered, all instrumental titrations aim, in principle, to obtain the Veq value on the basis of experimental data {(Vj, yj) | j = 1,…,N}, where y = pH, E for potentiometric methods of analysis. Referring to Eq. (22), we have
C0.V0 = 103 . mA/MA (24)
where mA [g] and MA [g/mol] denote mass and molar mass of analyte (A), respectively. From Eqs. (22) and (24), we get
mA = 10-3. C . MA. V/Φ (25)
The value of the fraction V/Φ in Eq. (25), obtained from Eq. (22),
V/Φ = C0. V0/C (26)
is constant during the titration. Particularly, at the end (e) and equivalent (eq) points we have
V/Φ = Ve/Φe = Veq/Φeq (27)
The Ve [mL] value is the volume of T consumed up to the end (e) point, where the titration is terminated (ended). The Ve value is usually determined in visual titration, when a pre-assumed color (or color change) of D+T mixture is obtained. In a visual acid-base titration, pHe value corresponds to the volume Ve [mL] of T added from the start for the titration and
C . Ve
Φe= ------------ (28)
C0. V0
is the Φ-value related to the end point. From Eqs. (25) and (27), one obtains:
(a) mA = 10-3.C.Ve.MA/Φe and (b) mA = 10-3.C.Veq.MA/Φeq (29)
This does not mean that we may choose between Eqs. (29a) and (29b), to calculate mA. Namely, Eq. (29a) cannot be applied for the evaluation of mA: Ve is known, but Φe unknown. Calculation of Φe needs prior knowledge of C0 value; e.g., for the titration system NaOH(C,V) → HCl(C0,V0) we have [2]
Φe= C/C0. (C0 - αe) / (C+αe) (30)
where: α = [H+1] – [OH-1] = 10-pH – 10pH-14, and αe = α(pHe). However, C0 is unknown before the titration; otherwise, the titration would be purposeless. The pHe value in visual titration is known only approximately. Also Eq. (29b) is useless: the ‘round’ Φeq value is known exactly, but Veq is unknown; Ve (not Veq) is determined in visual titrations.
Because Eqs: (29a) and (29b) appear to be useless, the third, approximate formula for mA, has to be applied[19], namely:
mA' = 10-3.C.Ve.MA/Φeq = 10-3.C.Ve.MA.RAeq (31)
where Φeq is put for Φe in Eq. 29a, and
RAeq = MA/Φeq (32)
is named as the equivalent mass. The relative error in accuracy, resulting from this substitution, equals to
δ = (mA’ – mA)/mA = mA’/mA – 1 = Ve/Veq – 1 = Φe/Φeq – 1 (33)
In particular, for the titration of V0 = 100 mL of C0 = 0.01 mol/L A = Br2 (MBr2 = 159.808 g/mol) with V mL of C = 0.1 mol/L NaOH we have Φeq = 2 (see Table 2). At pH = pHe = 9.413 we have Φe = 2.003, and then δ = 2.003/2 – 1 = 0.15%. Note that this result was obtained on the basis of thermodynamic knowledge (GATES/GEB), not from invalid, stoichiometric considerations.
Some remarks related to balances
Equations and equalities
Among the concentration balances one can distinguish equations and equalities. An equality, represented by the relation (14a), involves only one species, whereas an equation involves more species, see e.g. Eq. (13a) or Eq. (16a). Concentrations of the species in the balances are involved in expression(s) for the corresponding equilibrium constant(s), exemplified by the relations presented in Table 1. In the equality (14a), the value for [Na+1] is a number for the pre-assumed C and V0 values, at given V-value; as such, it can enter immediately the related ChB, see Eq. (9c). Then (14a) is not considered as equation, when the number of equations is compared with the number of independent variables.
Table 1. Equilibrium data related to different bromine species.
| No. | Reaction | Equilibrium equation | Equilibrium data |
|---|---|---|---|
| 1 | BrO3–1+6H+1+6e–1 = Br–1+3H2O | [Br–1] = Ke1•[BrO3–1][H+1]6[e–1]6 | E04 = 1.45 V |
| 2 | BrO–1+H2O+2e–1 = Br–1+2OH–1 | [Br–1] = Ke2•[BrO–1][H+1]2[e–1]2/KW2 | E03 = 0.76 V |
| 3 | Br2+2e–1 = 2Br–1 | [Br–1]2 = Ke3•[Br2][e–1]2 | E03 = 1.087 V |
| 4 | Br3–1+2e–1 = 3Br–1 | [[Br–1]3 = Ke4•[Br3-1][e–1]2 | E04 = 1.05 V |
| 5 | HBrO3 = H+1+BrO3–1 | [H+1][BrO3-1] = K51•[HBrO3] | pK51= 0.7 |
| 6 | HBrO = H+1+BrO-1 | [H+1][BrO-1] = K11•[HBrO] | pK11 = 8.6 |
| 7 | H2O = H+1+OH-1 | [H+1][OH–1] = KW | pKW = 14.0 |
| where: logKe1 = 6AE01, logKei = 2AE0i (i = 2,3,4); A = 16.9; pK51 = -logK51, pK11 = -logK11, pKW = -logKW | |||
Table 2: The sets of (Φ, pH, E) values taken from the vicinity of the equivalence points for the Systems 1 and 2, at V0 = 100, C0 = 0.01, C = 0.1.
| System 1 | System 2 | |||||
|---|---|---|---|---|---|---|
| NaOH (C,V)→Br2 (C0,V0) | NaOH (C,V) →HBrO (C0,V0) | |||||
| Φ | pH | E | Φ | pH | E | |
| 1,995 | 6,666 | 1,0491 | 0,995 | 6,347 | 1,0720 | |
| 1,996 | 6,728 | 1,0455 | 0,996 | 6,411 | 1,0681 | |
| 1,997 | 6,811 | 1,0406 | 0,997 | 6,498 | 1,0630 | |
| 1,998 | 6,933 | 1,0334 | 0,998 | 6,625 | 1,0555 | |
| 1,999 | 7,161 | 1,0199 | 0,999 | 6,866 | 1,0412 | |
| 2,000 | 8,143 | 0,9619 | 1,000 | 8,102 | 0,9682 | |
| 2,001 | 8,966 | 0,9132 | 1,001 | 9,002 | 0,9150 | |
| 2,002 | 9,244 | 0,8968 | 1,002 | 9,281 | 0,8985 | |
| 2,003 | 9,413 | 0,8868 | 1,003 | 9,450 | 0,8885 | |
| 2,004 | 9,534 | 0,8797 | 1,004 | 9,571 | 0,8814 | |
| 2,005 | 9,628 | 0,8741 | 1,005 | 9,666 | 0,8758 | |
Number of independent equations and dependency/independency property
In the System 1, three equations: (9c), (13a) and (16a) form a set of independent[20,21] equations. In this context, four equations: (9c), (13a), (16a) and (17a)
(ZBr–5).([HBrO3]+[BrO3-1])+(ZBr–1).([HBrO]+[BrO-1])+2ZBr.[Br2]+(3ZBr+1).[Br3-1]+(ZBr+1).[Br-1] = 2ZBr.C0 (17a)
form a set of linearly dependent equations in the System 1; in other words, the set of equations: {(9c), (13a), (16a)} or {(9c), (13a), (17a)} can be chosen, optionally, as the equations involved in the algorithm applied for calculation purposes, see Appendix, where Eq. (17a) is involved. In the Systems 1 and 2, three independent variables: xT = (x(1), x(2), x(3)) = (E, pH, pBr) are involved. Informally, for the System 1, E is ascribed to GEB (Eqs. (16a),(17a)), pH to ChB (Eq. (9c)), and pBr – to the concentration balance for Br (Eq. (13a)). The volume V of the titrant (T) added is considered as a parameter, not variable; the V value is changed, in steps, in the calculation procedure, realized according to iterative computer program, here: MATLAB.
The linear dependence of algebraic equations is usually checked using the Gaussian elimination method[22] or the Kronecker-Capelli theorem[23]; there are time-consuming procedures, however. Afar most efficient method of the linear combination is presented[20], where the set of dependent equations related to non-redox systems is reduced to the identity 0 = 0, whereas the simplest form of the linear combination is obtained for redox systems[20,24]; high efficiency of this method can easily be checked in far more complex electrolytic non-redox or redox systems, also in mixed-solvent media[25-27].
Oxidation number, oxidant and reductant as the redundant terms
In formulation of GEB according to the Approach II to GEB, the prior knowledge of oxidation numbers is not needed; it is the paramount advantage of the Approach II to GEB, particularly when applied to complex organic species, with radicals and ion-radicals involved. It should be noticed that the oxidation number, representing the degree of oxidation of an element in a compound or a species, is a contractual concept. None prior knowledge, except composition and external charge of the species formed in the system is needed. The equivalency of the Approaches I and II to GEB means that the equation obtained by a suitable linear combination of pr-GEB with charge balance and other elemental/core balances becomes identical with the one obtained directly from the Approach I to GEB.
The GEB related to the System 1 with Br2 (C0) and expressed by Eq. (16a), obtained according to Approach II to GEB, can be rewritten as follows:
1.(+5).([HBrO3]+[BrO3-1])+1.(+1).([HBrO]+[BrO-1])+2.0.[Br2]+3.(–1/3).[Br3-1]+1.(–1).[Br-1] = 2.(0).C0V0/ (V0+V) (16b)
whereas the GEB related to the System 2 with HBrO (C0) and expressed by Eq. (20a), obtained according to Approach II to GEB, can be rewritten as follows:
1.(+5).([HBrO3]+[BrO3-1])+1.(+1).([HBrO]+[BrO-1])+2.0.[Br2]+3.(–1/3).[Br3-1]+1.(–1).[Br-1] = 1.(1).C0V0/(V0+V) (20b)
Analogous balances are obtained for static systems, with C0mol/L (a) Br2, (b) HBrO. As we see, the coefficients at the concentrations of the corresponding species and at the concentrations of the related components are equal to the oxidation numbers of Br as an electron-active component in the related Systems (1 and 2).
It is a general property, valid also in the systems where two or more electron-active elements are involved.
We refer here to titration of V0 mL of the titrand D containing FeSO4 (C0)+H2SO4 (C01) with V mL of titrant T, containing KMnO4(C), added up to a given point of the titration. In this case, the linear combination of electron-non-active elements (‘fans’), expressed as follows[28]
2.f(O) – f(H) + ChB – f(K) – 6.f(SO4) = – (f(H) – 2.f(O) + f(K)+6.f(SO4) – ChB) ↔ (+1).f(H) + (–2).f(O) + (+1).f(K)+(+6).f(SO4) – ChB → (34)
(+2).([Fe+2]+[FeOH+!]+[FeSO4])+(+3).([Fe+3]+[FeOH+2]+[Fe(OH)2+1]+2[Fe2(OH)2+4]+[FeSO4+1]+[Fe(SO4)2-1])+(+2) . ([Mn+2]+[MnOH+1]+[MnSO4])+(+3).([Mn+3]+[MnOH+2])+γ.(+4).[MnO2]+(+6) . [MnO4-2]+(+7) . [MnO4-1] = (+2) . C0V0/ (V0+ V)+(+7) . CV/ (V0+ V) (34a)
where γ = 1 if precipitation of MnO2 in this system is admitted (e.g. at too small C01 value), or γ = 0 if it does not occur. The simplest form of GEB is obtained there from linear combination of the above balance (34) with the balances for the electron-active elements (‘players’). At γ = 0 we have[29-32]
(+1).f(K)+(+6).f(SO4)+(+3).f(Fe)+(+2).f(Mn)+(–2).f(O)+(+1).f(H) – ChB (35)
[Fe+2]+[FeOH+1]+[FeSO4] – (5[MnO4-1]+4[MnO4-2]+[Mn+3]+[MnOH+2]) = (C0V0 – 5CV)/(V0+V) (35a)
This property is also related to non-redox systems.
We refer here to V0 mL of CuSO4 solution prepared from N01 molecules of CuSO4•5H2O and N02 molecules of H2O. The resulting solution consists of the following species: H1O (N2), H+1 (N2, n2), OH-1 (N3, n3), HSO4-1 (N4, n4), SO4-2 (N5, n5), Cu+2 (N6, n6), CuOH+1 (N7, n7), Cu(OH)2 (N8, n8), Cu(OH)3-1 (N9, n9), Cu(OH)4-2 (N10, n10), CuSO4 (N11, n11). The components and species are involved in the balances for particular elements: H, O, Cu, S, i.e.,
f1 = f(H) : 2N1+N2(1+2n2)+N3(1+2n3)+N4(1+2n4)+N52n5+N62n6+N7(1+2n7)+N8(2+2n8)+N9(3+2n9)+N10(4+2n10)+N112n11 = 10N01+2N02 (36)
f2 = f(O) : N1+N2n2+N3(1+n3)+N4(4+n4)+N5(4+n5)+N6n6+N7(1+n7)+N8(2+n8)+ N9(3+n9)+N10(4+n10)+N11(4+n11) = 9N01+N02 (37)
f12 = 2.f(O) – f(H) : –N2+N3+7N4+8N5+N7+2N8+3N9+4N10+8N11 = 8N01 (38)
f0 = ChB : N2 – N3 – N4 – 2N5+2N6+N7 – N9 – 2N10 = 0 (39)
–2f3 = – 2f(Cu) : 2N01 = 2N6+2N7+2N8+2N9+2N10+2N11 (40)
–6f4 = – 6f(S) = – 6f(SO4): 6N01 = 6N4+6N5+6N11 (41)
Simple addition of the elemental/core balances 38 – 41 gives the identity
2.f(O) – f(H)+ChB – 2f(Cu) – 6f(S) = 0 => (+1).f(H)+(–2).f(O)+(+2).f(Cu)+(+6).f(S) – ChB = 0 => 0 = 0 (42)
As we see, at the identity condition fulfilled, the multipliers in the transformed identity are equal to oxidation numbers of the indicated elements.
As results from the examples presented above,
(1) Formulation of GEB according to Approach II to GEB needs none prior knowledge of the oxidation states (oxidation numbers) of all elements participating the System 1 or 2, i.e., Br, H, O; it means that the oxidation state (oxidation number) is the derivative concept within GATES/GEB;
(2) The terms: oxidant and reductant are not distinguished, i.e., not ascribed a priori to particular components and species in electrolytic systems, considered according to GATES/GEB principles, with GEB obtained according to Approaches I and II to GEB; full ‘democracy’ in this respect is assumed;
(3) In the balance obtained from f12+f0, the oxidation numbers in particular Br-species are equal to (or involved with) the coefficient/multiplier at the concentration of the corresponding species with electron-active element (here: Br), and in the component (Br2 or HBrO) or bromine species. If the species or component involves more atoms of an electron-active element, then the coefficient is equal to the product of the related numbers; e.g. –[Br3-1] = 3.(–1/3).[Br3-1] in Eq. 16a or 20a, where 3 – number of Br-atoms, –1/3 – oxidation number of Br in Br3-1.
Concluding remarks
The unique property of 2.f(O) – f(H)
In all instances it can be stated that – for all redox systems – any linear combination of f12 = 2.f(O) – f(H) with f0 = ChB and other elemental/core[20] balances related to a redox system of any degree of complexity does not give the identity, see e.g. Eqs. (16a) or (20a) are different from identity 0 = 0, of course.
The redox systems are ‘coded’ in the respective balances: f(H) and f(O). The balance 2.f(O) – f(H) is linearly independent on charge and concentration balances related to redox systems, and it is dependent on those balances when related to non-redox systems. The independency or dependency property is then the general criterion distinguishing between redox and non-redox systems[11-20], of any degree of complexity, also in mixed-solvent media[25-27]. This unique, general property explains clearly why the elemental balances: f(H) and f(O) are not formulated in any non-redox system. This regularity applies to non-redox systems of any degree of complexity, both for systems with aqueous solutions, as well as with amphiprotic solvents or a mixture of solvents, including at least one amphiprotic co-solvent[21]. The 2.f(O) – f(H) and any linear combination of 2.f(O) – f(H) with charge balance and other (elementary, core) balances of a given system retain full properties of the GEB.
Contrary to appearances, established by the current paradigm, this criterion distinguishing non-redox and redox systems and unknown in earlier literature, is not immediately/explicitly associated with free electrons in the system. It provides a kind of uniformity in the formulas derived for this purpose. This fact, especially the simple calculations of free electron concentrations in redox systems[5], deny the unique role of free electrons in redox reactions, expressed in elementary redox reactions, as described in half- or partial reactions, where the species of the same element with different oxidation numbers are involved.On the other hand, it points to the unique role of H and O in redox systems[33-41], suggested in earlier theoretical/hypothetical considerations on these systems. This issue will be developed in a separate work.
Before 1992, the basic property of the balance 2.f(O) – f(H) for redox systems was unknown at all in scientific world, and the linear independency/dependency of 2.f(O) – f(H) as the fundamental/practical criterion distinguishing redox/non-redox systems of any degree of complexity was also unknown. Here is the hidden simplicity, which had to be discovered, as the Approach II to GEB. One of the authors™ contends that the discovery of the Approach II GEB would most likely be impossible without the prior discovery of the Approach I to GEB. The Generalized Electron Balance (GEB) concept, valid for redox electrolytic systems, is the emanation of balances for H and O, referred to aqueous media. GEB is compatible with other (charge and concentration) balances and enables to resolve the electrolytic (mono- or/and two-phase) redox systems of any degree of complexity, within the scope of Generalized Approach To Electrolytic Systems (GATES), perceived as the thermodynamic approach to equilibrium and metastable systems, where all necessary physicochemical knowledge on the systems tested is involved. The advantages of GATES are illustrated on examples of redox and non-redox analytical systems. The GATES is perceived as the unrivalled tool applicable, among others: (a) to mathematical modelling of thermodynamic behavior of the systems, (b) in choice of optimal a priori conditions of chemical analyses, and (c) in gaining chemical information invisible in real experiments, in general. Furthermore, GATES is the basis for Generalized Equivalence Mass (GEM) concept, considered as the advantageous alternative against the obligatory Equivalence Mass (EM) concept suggested by IUPAC. According to GATES, any chemical reaction notation is only a basis to formulate the related expression for equilibrium constant according to mass action law.
GATES/GEB allows tracking not only the individual titrations, but also the processes composed of several steps, as shown in the example of iodometric determination of copper[5]. The entire analytical process is partitioned here into 4 stages: two preparatory stages, with non-redox reactions, and two further stages in which redox reactions occurred. The majority of the dynamic systems, realized according to titrimetric mode, are perceived also as an important tool in the classical chemical analysis.
GATES/GEB is a counter-proposal in relation to earlier IUPAC decisions, presented in three subsequent editions of the Orange Book, and based on reaction stoichiometry; that viewpoint was criticized unequivocally/exhaustively/convincingly, especially in a series of review articles[2-5]. It was demonstrated, on examples of redox systems of different complexity, that stoichiometry is a secondary/derivative concept from the viewpoint of GATES, and GATES/GEB, in particular.
Concluding, GATES is the overall, thermodynamic approach to redox and non-redox, static and dynamic, single and multiphase equilibrium, metastable and non-equilibrium electrolytic systems, of any degree of complexity. Possibilities of GATES/GEB are far greater than ones offered by the actual physicochemical knowledge related to the system in question.
Appendix
Computer program for the NaOH_Br2 system
function F = NaOH_Br2(x)
global V C0 V0 C yy
E = x(1);
pH = x(2);
pBr = x(3);
H = 10^(-pH);
Kw = 10^-14;
pKw = 14;
OH = Kw/H;
A = 16.92;
Br = 10^-pBr;
ZBr = 35;
Br2 = Br^2*10^(2*A*(E-1.087));
Br3 = Br^3*10^(2*A*(E-1.05));
BrO = Br*10^(2*A*(E-0.76)+2*pH-2*pKw);
BrO3 = Br*10^(6*A*(E-1.45)+6*pH);
HBrO = 10^8.6*H*BrO;
HBrO3 = 10^0.7*H*BrO3;
Na = C*V/(V0+V);
F = [%Charge balance
(H-OH+Na-Br-Br3-BrO-BrO3);
%Concentration balance for Br
(Br+3*Br3+2*Br2+HBrO+BrO+HBrO3+BrO3 - 2*C0*V0/ (V0+V));
%Electron balance
((ZBr+1)*Br+(3*ZBr+1)*Br3+2*ZBr*Br2+(ZBr-1)*(HBrO+BrO)...
+(ZBr-5)*(HBrO3+BrO3) - 2*ZBr*C0*V0/ (V0+V))];
yy(1) = log10(Br);
yy(2) = log10(Br3);
yy(3) = log10(Br2);
yy(4) = log10(HBrO);
yy(5) = log10(BrO);
yy(6) = log10(HBrO3);
yy(7) = log10(BrO3);
yy(8) = log10(Na);
References
[1] Michalowski, T. The Generalized Approach to Electrolytic Systems: I. Physicochemical and Analytical Implications. (2010) Critic Rev Analyl Chem 40(1): 2-16.
[2] Michalowski, T., Pietrzyk, A., Ponikvar-Svet, M., et al. The Generalized Approach to Electrolytic Systems: II. The Generalized Equivalent Mass (GEM) Concept. (2010) Critic Rev Analyl Chem 40(1): 17-29.
[3] Michalowska-Kaczmarczyk, A.M., Asuero, A.G., Michalowski, T., et al. “Why not stoichiometry” versus “Stoichiometry – why not?” Part I: General context. (2015) Critic Rev Analyl Chem 45(2): 166–188.
[4] Michalowska-Kaczmarczyk, A.M., Asuero, A.G., Toporek, M., et al. “Why not stoichiometry” versus “Stoichiometry – why not?” Part II: GATES in context with redox systems. (2015) Critic Rev Analyl Chem 45(3): 241–269.
[5] Michalowska-Kaczmarczyk, A.M., Michalowski, T., Toporek, M. et al. “Why not stoichiometry” versus “Stoichiometry – why not?” Part III, Extension of GATES/GEB on Complex Dynamic Redox Systems. (2015) Critic Rev Analyl Chem 45(4): 348-366.
[6] Karen, P., McArdle, P., Takats, J. Comprehensive definition of oxidation state (IUPAC Recommendations 2016). (2016) Pure Appli Chem 88(8): 831-839.
[7] Karen, P. Oxidation state, a long-standing issue! (2015) Angew Chem Int Ed Engl 54(16): 4716-4726.
[8] Karen, P., McArdle, P., Takats, J. Toward a comprehensive definition of oxidation state (IUPAC Technical Report). (2014) Pure Appli Chem 86(6): 1017-1081.
[9] Michalowski, T. Application of GATES and MATLAB for Resolution of Equilibrium, Metastable and Non-Equilibrium Electrolytic Systems. (2011) Chem Eng Tech 1-34.
[10] Michalowski T. Applications of MATLAB in Science and Engineering. (2011) InTech-Open science.
[11] Michalowski, T., Toporek, M., Michalowska-Kaczmarczyk, A.M., et al. New Trends in Studies on Electrolytic Redox Systems. (2013) Electrochimica Acta109: 519-531.
[12] Michalowski, T., Michalowska-Kaczmarczyk, A.M., Toporek, M., et al. Formulation of general criterion distinguishing between non-redox and redox systems. (2013) Electrochimica Acta 112: 199-211.
[13] Michalowska-Kaczmarczyk, A.M., Toporek, M., Michalowski, T., et al. Speciation Diagrams in Dynamic Iodide+Dichromate System. (2015) Electrochimica Acta 155: 217–227.
[14] Toporek, M., MichalowskaKaczmarczyk, A.M., Michalowski, T., etal. Symproportionation versus Disproportionation in Bromine Redox Systems. (2015) Electrochimica Acta 171: 176–187.
[15] Michalowska-Kaczmarczyk, A.M., Asuero, A.G., Toporek, M., et al. “Why not stoichiometry” versus “Stoichiometry – why not?” Part II: GATES in context with redox systems. (2015) Critic Rev Analy Chem 45(3): 240–268.
[16]Lurie, Yu Handbook of Analytical Chemistry. (1975) Mir Publishers Moscow.
Pubmed || Crossref || Others
[17] Michalowski, T. Calculation of pH and potential E for bromine aqueous solutions. (1994) J Chemic Edu 71(7): 560-562.
[18] Michalowski, T., Lesiak, A. Acid-base titration curves in disproportionating redox systems. (1994) Journal of Chemical Education 71(8): 632-636.
[19] Asuero, A.G., Michalowski, T. Comprehensive formulation of titration curves referred to complex acid-base systems and its analytical implications. (2011) Critic Rev Analy Chem 41(2): 151-187.
[20] Michalowska-Kaczmarczyk, A.M., Michalowski, T. Comparative balancing of non-redox and redox electrolytic systems and its consequences. (2013) American J Analytical Chem 4(10): 46-53.
Pubmed || Crossref || Others
Pubmed || Crossref || Others
Pubmed || Crossref || Others
[24] Michalowska-Kaczmarczyk, A.M., Spórna-Kucab, A., Michalowski, T. Generalized Electron Balance (GEB) as the Law of Nature in Electrolytic Redox Systems, in: Redox: Principles and Advanced Applications, Ali Khalid, M.A. (Ed.) (2017) InTech Chap. 2, 10-55.
[25] Michalowska-Kaczmarczyk, A.M., Michalowski, T., et al. Linear Dependence of Balances for Non- Redox Electrolytic Systems. (2014) Ameri J Analy Chem 5: 1285-1289.
[26] Michalowska-Kaczmarczyk, A.M., Michalowski, T., et al. Generalized Electron Balance for Dynamic Redox Systems in Mixed-Solvent Media. (2014) J Analyt Sci Meth Inst 4(4): 102-109.
[27] Michalowski, T., Pilarski, B., Asuero, A.G., et al. Modeling of Acid-Base Properties in Binary-Solvent Systems. (2010) Talanta 80(3): 1073-1080.
[28] Michalowska-Kaczmarczyk, A.M., Spórna-Kucab, A., Michalowski, T., et al. A general property differentiating between redox and non-redox electrolytic systems and its consequences. (2017) Int J Math Statist Inv 6(3): 67-76.
Pubmed || Crossref || Others
[29] Michalowski, T., Baterowicz, A., Madej, A., et al. An extended Gran method and its applicability for simultaneous determination of Fe(II) and Fe(III). (2001) Analytica Chimica Acta 442(2): 287-293.
[30] Michalowski, T., Toporek, M., Rymanowski, M. Overview on the Gran and other linearization methods applied in titrimetric analyses. (2005) Talanta 65(5): 1241-1253.
[31] Michalowski, T., Kupiec, K., Rymanowski, M. Numerical analysis of the Gran methods A comparative study. (2008) Analytica Chimica Acta 606(2): 172-183.
[32] Ponikvar, M., Michalowski, T, Kupiec, K., et al. Experimental verification of the modified Gran methods applicable to redox systems. (2008) Analytica Chim Acta 628(2): 181-189.
[33] Michalowska-Kaczmarczyk, A.M., Michalowski, T. GATES as the Unique Tool for Simulation of Electrolytic Redox and Non-Redox Systems. (2014) J Anal & Bioanal Tech 5:204
[34] Michalowska-Kaczmarczyk, A.M., Spórna-Kucab, A., Michalowski, T. A Distinguishing Feature of the Balance 2.f(O) – f(H) in Electrolytic Systems. The Reference to Titrimetric Methods of Analysis, in: Advances in Titration Techniques. (2017) InTech Chap 6: 174-207.
[35] Michalowska-Kaczmarczyk, A.M., Spórna-Kucab, A., Michalowski, T. Principles of Titrimetric Analyses According to GATES, in: Advances in Titration Techniques. (2017) InTech Chap 5: 133-171.
[36] Michalowska-Kaczmarczyk, A.M., Spórna-Kucab, A.,Michalowski, T. Solubility products and solubility concepts, in: Descriptive Inorganic Chemistry. Researches of Metal Compounds. (2017) InTech Chap 5: 93-134.
[37] Meija, J., Michalowska-Kaczmarczyk, A.M., Michalowski, T. Redox titration challenge. (2017) Anal Bioanal Chem 409(1): 11–13
[38] Michalowski, T., Michalowska-Kaczmarczyk, A.M., Meija, J. Solution of redox titration challenge. (2017) Anal Bioanal Chem 409(17): 4113-4115.
[39] Michalowska-Kaczmarczyk, A.M., Spórna-Kucab, A., Michalowski, T. Formulation of simple electrolytic redox systems according to GATES/GEB principles. (2017) J Chem Appl Chem Eng 1:1.
Pubmed||Crossref||Others
[40] Michalowska-Kaczmarczyk, A.M., Spórna-Kucab, A., Michalowski,T. DynamicBufferCapacities in Redox Systems. (2017) J Chem Appl Chem Eng (2017) 1:2
Pubmed||Crossref||Others
[41] Michalowska-Kaczmarczyk,A.M., Spórna-Kucab, A., Michalowski, T. Oxidation number, oxidant and reductantas derivative concepts within GATES/GEB formulation. (2017) J Chem Appl Chem Eng 1:2
Pubmed||Crossref||Others