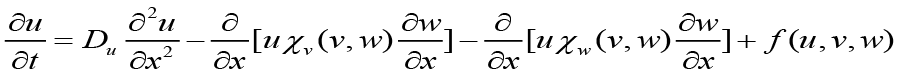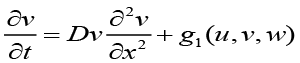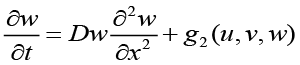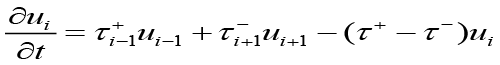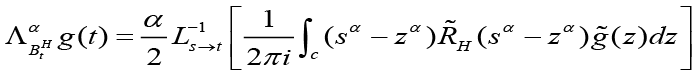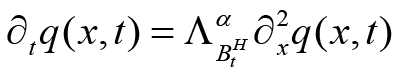An essential characteristic of living organisms is the ability to sense signals in the environment and adapt their movement accordingly^[1].” Microbes are defined as microscopic organisms, such as bacteria, viruses, protozoa and etc. For practicality focus is limited to bacteria. These single-celled microscopic organisms are capable of reproduction and motility, and they control their pathogenicity in accordance to their local population density by movement and by regulation of cellular reproduction. Bacterial populations perform some genetic functionalities that one bacterial cell may not be able to accomplish alone, such as bio-luminescence, attacking a host, or assimilating into specific patterns to create structures, bio-films and etc. According to Purcell^[2] bacterial cells live in an environment at a low Reynolds number which renders their inertia as an irrelevant factor in their motion. This results in simplifying the analysis to the individual cell motion, and this motion is limited by the ability of the flagella to propel them symmetrically, imparting Brownian motion. Escherichia Coli (E.Coli) bacteria have flagella that rotate by a biochemically powered motor located close to the body. Because of the chirality of these flagella, their clockwise and anti-clockwise rotations are nonequivalent. One rotation direction results in the flagella propelling the cell by creating a smooth swimming motion in one direction and the opposite rotation causes the flagella to separate, resulting in randomized cell motion as a binary response. We study such systems through a physics based approach and put forward the concepts and ideas which may be able to give us a much better understanding of such complex biological system.

Quorum Sensing and Chemotaxis

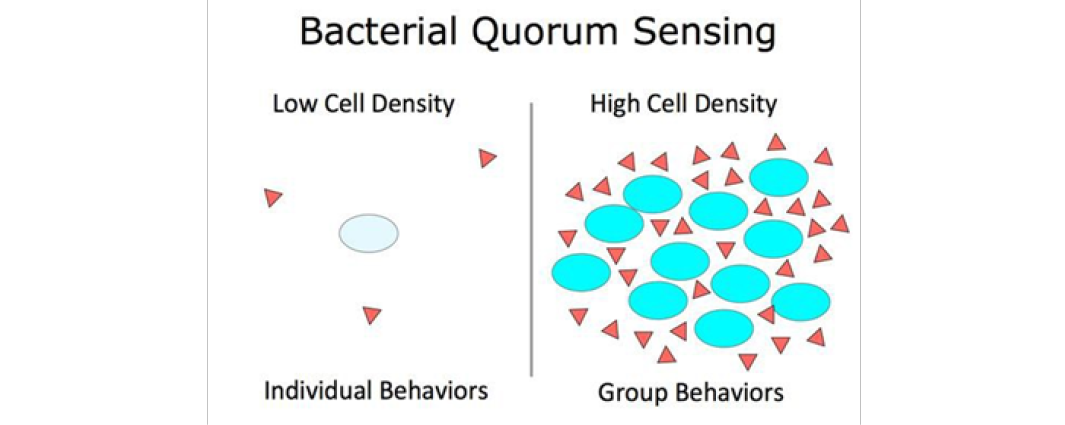
According to Bonnie Bassler^[3], Bacteria accomplish coordination of motion to perform multicellular functions via Quorum Sensing , a systematic production and reception of auto-inducers, or Quorum Sensing Molecules (QSM’s), to limit cell reproduction and therefore local population density. Certain physiological functions of bacteria can only be accomplished by many cells cooperating at once, and Quorum Sensing is how they detect and regulate their population. If each bacterial cell is in possession of 2 specific proteins on its surface, one producing QSM’s and another receiving the QSMs providing then the cell has access to information about the local QSM density, (see Figure 1). Once this local density of QSMs reaches a certain threshold, the cell can interpret an implicit population density threshold of other similar QSM producing cells signaling a stop in reproduction. This is a simplistic explanation of how cells of the same species regulate their local population densities based on a maximum threshold, which may rep- resent the population density required for some function or perhaps the maximum cell density the food (energy source) provided by the environment can support in a specific region.

Figure 1: QSM’s (triangles) and bacterial cells[3]

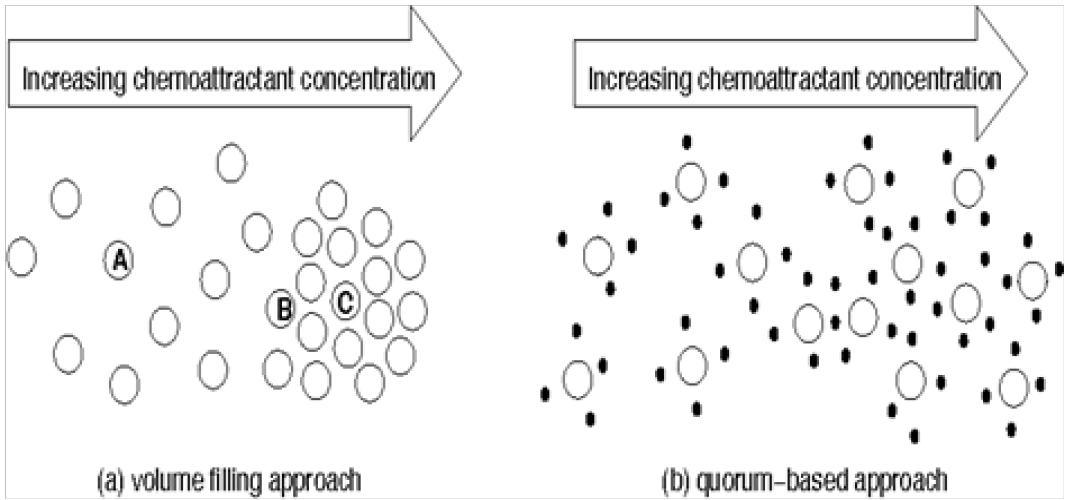
In addition to QSMs regulating bacterial behavior, the other important factors including Chemosensitive movement^[1], or response to chemicals in the environment as either Chemo- attractors or Chemo-repellants, Figure 2 are broadly used in the mathematical literature to represent motivating gradients such as food, predators, etc. Applying chemotactic sensitivity which is the extent to which a bacterial cells motion responds to the chemotactic gradient, and regulating this through population dynamics via quorum sensing the fundamentals involved in bacte- rial movement are understood. It is not purely Brownian motion as it retains global tendencies through these two concepts universal to bacteria. This Brownian motion can be expressed in terms of the Langevin equation from which we can calculate the entropy using Fokker-Planck equations. This will give us a better understanding of a non-equilibrium process and we can apply the same approach to other biological systems.

Figure 2: (1) Illustration of the (a) Volume filling model, and (b) Quorum sensing model

Multi-Fractal Brownian Motion

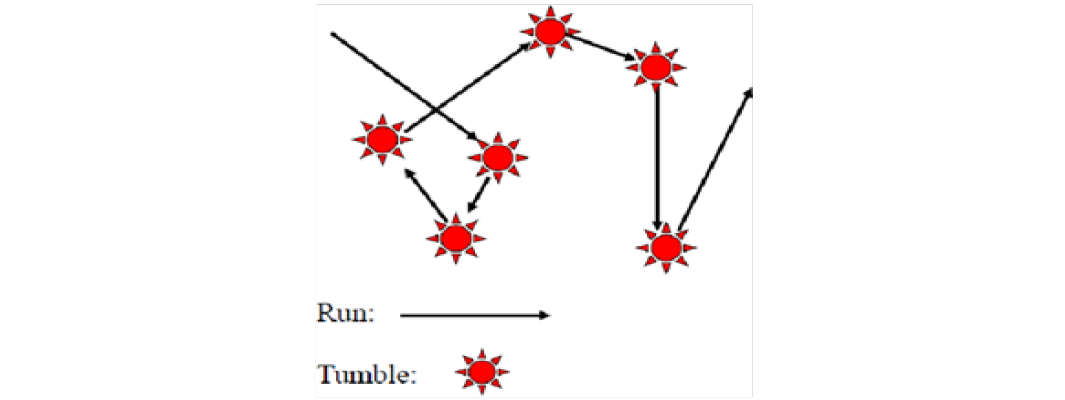
Restricting focus to Escherichia Coli (E.Coli), individual motions of bacterial cells are confined to a ”binary response”, specifically that of tumbles (randomizing their direction) or smooth runs (see Figure 3), ”In the presence of a chemo attractant, E. coli bias their behavior by tumbling less frequently in an increasing attractant gradient, resulting in the general movement towards high concentrations^[1].” This leads to a mathematical model by Kevin J. Painter and Thomas Hillen^[1] as a system of partial differential equations (see method section). Fig 3 Brownian Motion is described as a time evolution of a stochastic (random) process and is thus governed by the Fokker-Planck equation. In a general way the motion of a microbial organism is characterized but the motivation is to understand to what extent this can describe microbe movement and self-organization. Initially it was realized that a system of bacterial cells must be somewhat self-similar in their motion. This implies a degree of non-randomness. This realization prompted investigation into what is known as Fractional Brownian Motion fBm), which is used to model numerous mathematical outcomes in areas such as Finance, Hydrology, and Telecommunications^[5]. These processes are governed by the Hurst parameter. If a fractional Brownian process can be re-scaled to have stationary intervals, the Hurst exponent is regarded as a parametric constant characterizing the degree of self-similarity. If H = 1/2, the fBm is identical to a standard Brownian motion, if H > 1/2, the increments are persistent, if H < 1/2, the increments are anti-persistent. To take this one step further it is postulated that if a population of bacterial cells evolves through time in a non-linear way according to quorum sensing then the randomness of the individual cell motility must also vary. This conclusion was reached intuitively by considering the notion that chemo-sensitivity is a function of the population density of cells and by extension a function of QSM population dynamics. If the tumbling frequency and smooth walk duration are affected by chemo-sensitivity, then they are affected by population dynamics. Thus, the Hurst exponent characterizing the self-similarity of the motility processes of bacterial cells must vary in accordance with population growth, and in contrast to being a constant as in fractional Brownian motion, must in fact be variationally dependent on time. The final characterization of bacterial motion as Multi-Fractal Brownian Motion was determined by this realization. This a perturbation of the theory of stochastic processes, involving a time-varying Hurst parameter, H = H(t), which depicts the long-memory of a time series^[6]. Apparently, a bacterial cell population moves with a varying memory of past motion. This idea is corroborated by multiple peer reviewed papers^[5,7,8], and in fact a variation of the Fokker-Planck equation governing time evolutions of multi-fractal processes was found to have been derived in two concurring papers^[5,9]. The gap we discovered that has not been bridged, is between 1; the Fokker-Planck governing multi-fractal processes in junction with a time-varying Hurst parameter arising in bacterial population growth, and 2; a bacterial population dynamic governed by quorum sensing. We aim to use the mathematical modeling provided by the papers weave cited to bring quorum sensing into the fold of a progressive understanding of multi-fractal bacterial motility and swimming patterns generating bacterial grouping.

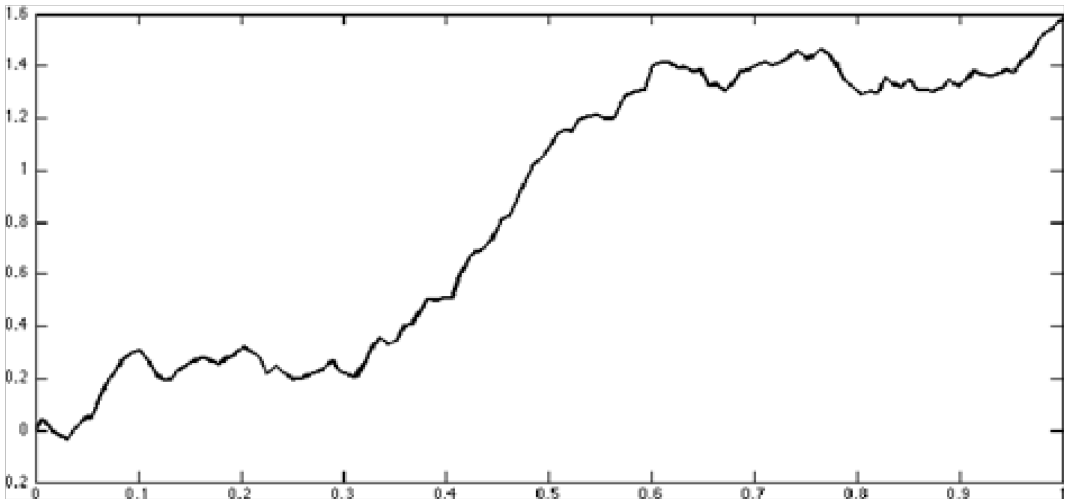
Figure 4 & 5 Exact sample paths of multi-fractal Brownian Motion with a various Hurst parameter functions H(t)^[5]

Figure 4: H(t) = .51 + (t.5)2 for t < .5 and H(t) = .51fort.5. The Hurst parameter approaches .51 as t_1/2

Figure 5: H(t) = 23 + sin(t)12. The Hurst parameter oscillates between 7/12 and 9/12

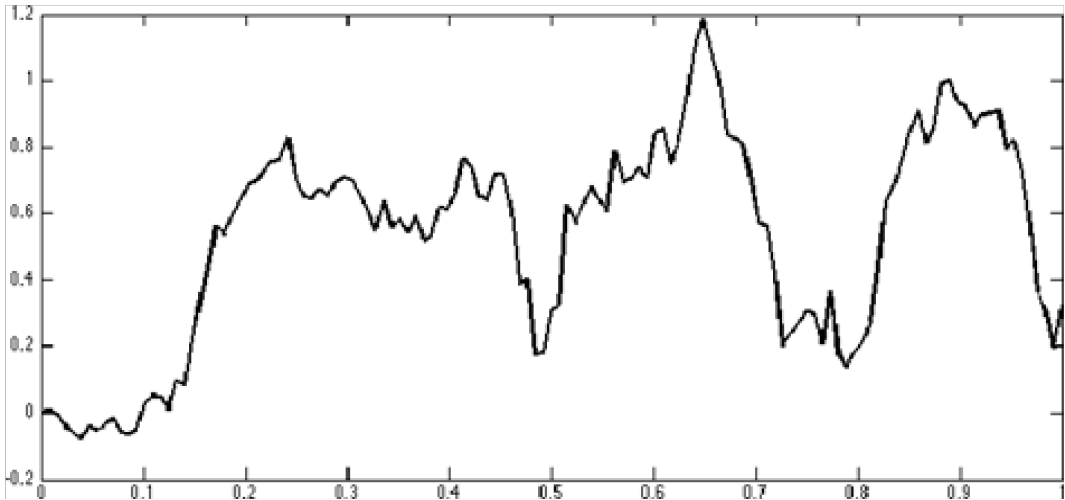
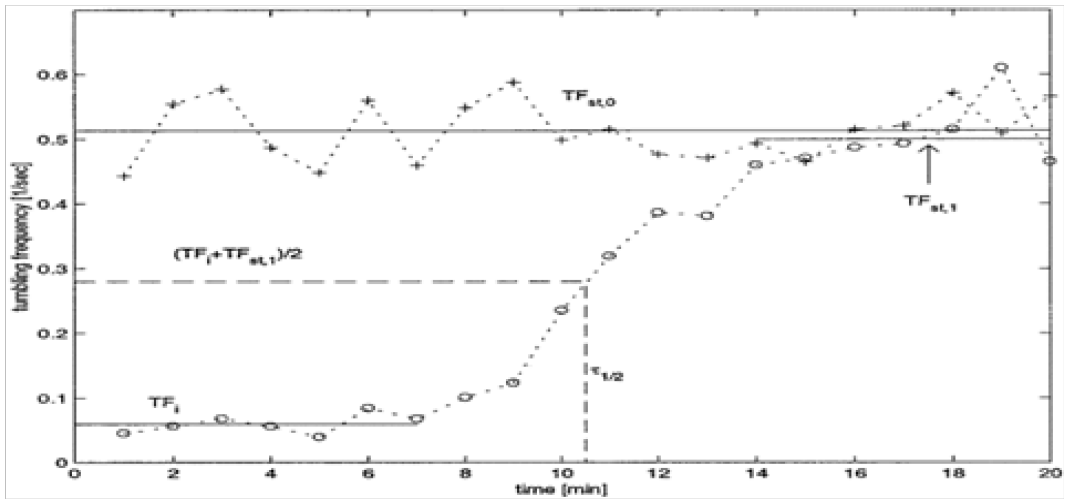
Note there is a striking resemblance between this sinusoidal Hurst parameter (Figure 4 5) and the graph describing tumbling frequency in a bacterial population (Figure 6). This suggests a direction for describing a time varying Hurst parameter as a function of population density.

Figure 6: Measurement of average tumbling frequency of stimulated and unstimulated cells. Average tumbling frequency of a cell population during a 10-s video segment was measured at 1-min intervals for 20 min after sample preparation^[8]. Cells at a given stage of growth were unstimulated (+) or stimulated with 1 mM L-aspartate (◦). The vertical dotted line corresponds to the time for 50% adaptation to a saturating stimulus of L-aspartate, τ_1/2. Other parameters described in the text are shown (T F_st,0, T F_i, and T F_st,1).

Contributions of Thermodynamics

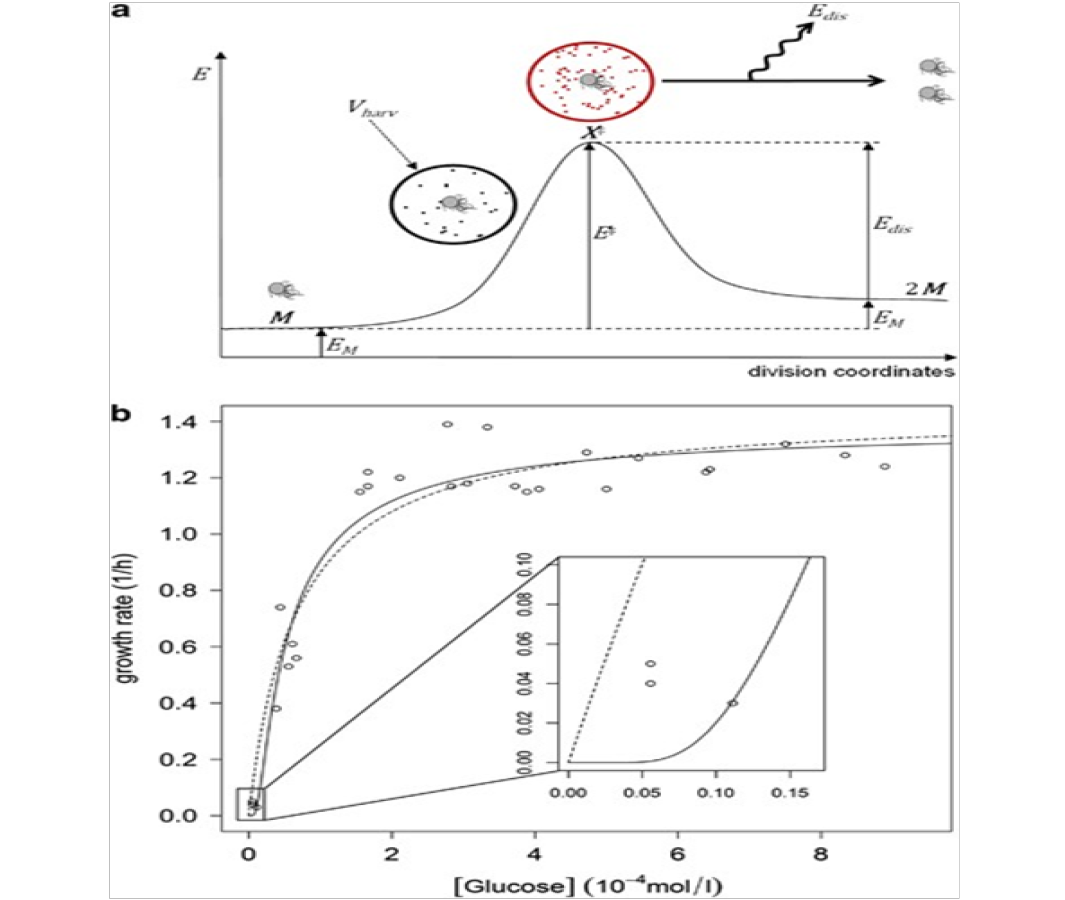
The fundamental assumption of statistical mechanics, as stated by Schroeder^[10], is that in an isolated system in thermal equilibrium all accessible microstates are equally probable. This leads him to assume that systems transitions between the available microstates are random and constitute no quantifiable pattern. It is here postulated that bacterial systems do generate observable patterns thus in a state of non-thermal equilibrium. Another principle detailed by Schroeder^[10] is that of ”Detailed Balance” which assumes that interactions between constituents of a system are strong enough for the exchange of energy, but too weak to have much effect on the energy levels themselves. According to M.E. Cates this principle of detailed balance is mesoscopically absent in motile bacteria^[4]. This implies that the interactions between bacterial cells must have a significant effect on the energy level of the system. Historically, modeling of the growth of microbes has relied on only empirical data, which limits understand- ing and predictive capacity in many environmental systems. Theoretically, a population of N bacterial cells are consuming food, transducing energy and reproducing. For each cell, it is proposed^[11] that consuming a threshold level of energy from the environment spontaneously triggers the transduction of the consumed energy in the division process increasing entropy and is thus an irreversible process (see Figure 7). During the harvesting process, each cell has access to a volume, V_harv , within which it can consume the chemical energy. The amount of energy available in V_harv for the cell to consume is dependent on the thermodynamic state of the environment, and is denoted as the ”catabolic energy”, representing the maximum amount of work available from the consumable molecules.

Figure 7: As shown in[11]; (a) Graphical representation of microbial energy levels along division coordinates. Microbial energy (E_M ) is augmented by the catabolic energy within the harvesting volume (E_cat[S]V_harv , symbolized as dots in a circle surrounding the microbe). Reaching the threshold catabolic energy (E_M + E ), the microbe is activated (a state denoted X ), and an irreversible division process is triggered, associated with energy dissipation (E_dis = E E_M ), resulting in two microbes. (b) Growth rate of E. coli as a function of glucose concentrations under aerobic conditions. The plain curve shows the fit of the data. The dashed curve shows the fit of a Monod equation. A detail of the growth rate/concentration dependency at low substrate concentration is shown, illustrating that the mathematical expression naturally accounts for the existence of an apparent substrate threshold concentration for growth.

A non-equilibrium thermodynamic state exists and the catabolic energy for each cell varies with time along with its chemotactic gradient. Energy levels can be attributed to each elementary volume V V_harv and thus to each cell. The existing kinetic theories describing microbial growth are all phenomenological in nature, and don’t treat the underlying metabolism. It would be impractical to write down all the kinetic theories specific to each enzyme reaction and integrate them individually.

An alternative approach is the consideration of these non-equilibrium processes through non-equilibrium thermodynamics, a case where more general expressions can be used to describe the heat evolution associated with microbial growth (E_dis in Figure 7), and in aerobic processes heat production is closely related to the rate of consumption of chemo-attractant (food) molecules^[9]. For more detailed chemistry information and the rigorous development of the “mosaic” approach see references^[9,11].

Mathematical Modeling

The first model of bacterial motion is one describing the population dynamics of all present factors that affect the tendencies in local individual cell movements. It is postulated that these population densities completely govern the statistics of how the bacterial cells will move. An initial Lotka-Volterra-type varying population differential equation is formulated. Response to the chemoattractant is regulated by the QSM density, providing a mechanism by which cells can pack at a lower density than the physical maximum to fill the local volume. The n’th cell’s transitional probability is of the general form, t(v, w) , where ”v” is the local chemoattractant density and ”w” is the local quorum-sensing molecule density. Different models are possible, depending on exactly how the quorum sensing modulates the signaling pathway, but assuming the case in which ”w” interferes with the gradient sensing the chemotactic sensitivity is

t = α + β(t (v_i±1, w_i±1) − t (v_i, w_i)) (1)

where α and β are constant parameters.

Assuming t ≥ 0 , where u_i(t) is the probability of a cell at idZ at time t, conditioned on beginning at i = 0 at t = 0. This evolution is placed into the continuous-time discrete-space equation^[1].

to achieve a system of coupled partial differential equations describing the population dynamics of bacteria, chemoattractant molecules, and QSM’s^[1].

Eq (3),

(4),

(5)

where

u(x, t) is the bacterial cell population density,

v(x, t) is the chemoattractant concentration,

w(x, t) is the QSM population density,

D_u,v,w are the diffusion coefficient related to the respective translational probabilities,

χ(v, w) = χ₀(1 − u) is commonly referred to as the chemotactic sensitivity function (as seen above, this is regulated both by QSM and Chemotaxis concentrations),

f, g1, g2 are additional chemical kinetics which account for the stochastic kinetics (random processes due to the low Reynolds-number environment).

Bacteria have been considered to be subject to Brownian motion as a consequence of the random kinetic processes imparted on them by their environment because of its high viscosity relative to their cell mass. As described here, these stochastic processes are not the only source of motion for bacteria. In the case of E. Coli cell motility is also self propagated via flagella in statistical accordance to genetic cooperation governed by perceived local population densities of QSM’s emitted by other cells and chemotactic gradients provided by the environment.This implies fractional Brownian motion, a Gaussian centered process [B_tH , t ≥ 0] with the covariance function 0 ≤ s, 0 ≤ t ,

E[B_tH B_sH ] = 1/2 (t2H + s2H − |t − s|2H ) (6)

where H d [0, 1], with a “Hurst parameter” H. If H = ½ we get E[B_t^½ B_s½ ] = t or s, and thus a completely unbiased random walk. Clearly, H m1/2, gives rise to the name “fractional” Brownian motion. This does not account for all of the tendencies implied by eqns (3), (4), (5). The bacterial cells move more(or less) randomly depending on where they are and how their environment has changed with time. As the cell population grows and moves, it affects its own chemotactic gradient and it also affects the statistical motility of its constituent cells via quorum sensing which governs local population densities. So, a given bacterial cell under such circumstances would clearly move more randomly in a time interval’s’ than in another time interval ’t’. IT is concluded that not only is the Hurst parameter H not constant and 1, it varies as a function of the QSM, bacterial, and chemotactic molecules population density, and thus is a function of time H = H(t). If H(t) is differentiable, then according to^[12], var[B_t^H ] = t^2Ht is differentiable and it is Laplace transformable. This satisfies the conditions for the derivation of a Fokker-Plank equation^[5]. Let B^H be a multifractional Brownian motion with H differentiable on (0, ∞), Eα be the inverse of a stable subordinator W with α d (0, 1), independent of BH. Then, the transition probabilities q(x, t) of the time-changed process (B_Et^αH )t ≥0 satisfy the Fokker-Plank partial differential equation^[5].

Eq (7)

where t > 0, x d R and ΛαBtH denoting the operator given by:

Eq (8)

with the initial condition q(x, 0) = δ(x) , where g˜(z) is the s → t Laplace transform of some function g(t) and L⁻¹_{s → t} is the inverse Laplace transform^[5,12].

Discussion

Throughout this paper the non-equilibrium statistical physics of microorganisms and its constituent mechanisms have been studied. It is possible for a general theory to exist, but it must be obtained by integrating multiple separate approaches to the subject; one of the goals of this effort. By inspecting the nature of quorum sensing and chemotactic behavior, it is concluded that bacterial motion can be identified as a multi-fractal Brownian process with a time-varying Hurst parameter, specific to any given species or collection of species. This classification prompted the investigation of a mathematical theory for the probability densities for various observables according to this particular time-varying behavior, and it was discovered that they can be generally considered as a class of functions satisfying the Fokker-Planck equations perturbation provided (eq. 5), which was derived and agreed upon by multiple sources^[5,9].

Acknowledgements: The authors thank Jackie Dunn of the physics & astronomy program, Department of Chemistry & Physics, Midwestern State University for useful discussions. The financial support of the Robert Welch Foundation (Grant #A0 − 0001) is gratefully acknowledged.

References

1. 1. Painer, K.J., Hillen, T. Volume-filling and quorum-sensing in models for chemosensitive movement. (2002) Canadian Appl Math Quart 10(4): 501-543.

   PubMed │CrossRef│Others

2. 2. Purcell, E.M. Life at low Reynolds number. (1977) Am J Phys 45(3)

   PubMed │CrossRef│Others

3. 3. Bassler, B.L. How bacteria talk to each other: regulation of gene expression by quorum sensing. (1999) Curr Opin Microbiol 2(6): 582 -587.

   PubMed │CrossRef│Others

4. 4. Cates, M.E. Diffusive transport without detailed balance in motile bacteria: does microbiology need statistical physics? (2012) Rep Prog Phys 75(4): 042601.

   PubMed │CrossRef│Others

5. 5. Ryvkina, J. Fractional Brownian Motion with Variable Hurst Parameter: Definition and Properties. (2013) J Theor Probability 28(3): 866-891.

   PubMed │CrossRef│Others

6. 6. Garcin, M. Estimation of time-dependent Hurst exponents with variational smoothing and application to forecasting foreign exchange rates. (2017) Physica A: statistical mechanics and its applications 483: 462-479.

   PubMed │CrossRef│Others

7. 7. Koorehdavoudi, H., Bogdan, P., Wei, G., et al. Multi-fractal characterization of bacterial swimming dynamics: a case study on real and simulated Serratia marcescens. (2017) Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 473.

   PubMed │CrossRef│Others

8. 8. Staropoli, J.F., Alon, U. Computerized Analysis of Chemotaxis at Different Stages of Bacterial Growth. (2000) Biophysical J 78(1): 513-519.

   PubMed │CrossRef│Others

9. 9. Westerhoff, H.V., Lolkema, J.S., Otto, R., et al. Thermodynamics of growth non-equilibrium thermodynamics of bacterial growth the phenomenological and the Mosaic approach. (1982) Biochimica et Biophysica Acta 683(3-4): 181-220.

   PubMed │CrossRef│Others

10. 10. Schroeder, D. An Introduction to Thermal Physics (Addison Wesley, 1999).

    PubMed │CrossRef│Others

11. 11. Que´me´ner, E. D-L., Bouchez, T. A thermodynamic theory of microbial growth. (2014) The ISME J 8(8): 1747-1751.

    PubMed │CrossRef│Others

12. 12. Hahn, M.G., Kobayashi, K., Umarov, S. Fokker-Planck-Kolmogorov equations associated with SDEs driven by time-changed fractional Brownian motion. (2010) Proc Amer Math Soc 139(2011): 691-705.

    PubMed │CrossRef│Others